بسم الله الرحمن الرحيم
السلام عليكم ورحمة
الله وبركاته ...
شرح درس
الحركة بتسارع منتظم – الحركة المتسارعة
نبدأ على بركة الله
...
السرعة المتجهة بدلالة التسارع المتوسط :
سبق في دراستنا أن
تطرقنا إلى مفهوم السرعة المتجهة وقمنا
بتعريفها وذكر كل من قانونها ووحدتها وقد فرقنا بينها وبين السرعة القياسية (عد
الى درس السرعة المتجهة في الفصل الثاني ) . كما سبق وتكلمنا عن التسارع وذكرنا
علاقته بالسرعة وكيف يمكن إيجاده وحساب قيمته .
في درس اليوم سنتعرف
على نوع من أنواع التسارع وهو التسارع المتوسط والذي يمكننا ببساطة وصفه بأنه سرعة
الجسم خلال فترة زمنية مقاسة .
·
تعريف التسارع المتوسط : مقدار التغير في السرعة المتجهة خلال الفترة الزمنية المقيسه ,
مقسوما على الفترة الزمنية .
·
يقاس التسارع المتوسط بوحدة : m/s2 .
·
رمزه: ᾱ
·
يمكننا استخدام التسارع المتوسط لتعيين مقدار
التغير في سرعة الجسم خلال فترة زمنية معينة
·
يعرف التسارع المتوسط بـالعلاقة :
·
يمكننا إعادة كتابة القانون السابق لإيجاد السرعة بدلالة كل من
التسارع المتوسط والفترة الزمنية : v = a t
vf - vi = a t
·
ولإيجاد السرعة النهائية نستخدم القانون التالي :
ونصها الفيزيائي هو : السرعة المتجهة النهائية تساوي السرعة المتجهة
الابتدائية مضافا إليها حاصل ضرب التسارع المتوسط في الفترة الزمنية .
·
ملاحظة : عندما يكون التسارع منتظم فإن التسارع المتوسط هو نفسه التسارع
اللحظي .
الموقع
بدلالة التسارع المنتظم :
·
الجسم الذي يتحرك بتسارع منتظم يغير سرعته المتجهة بمعدل منتظم .
الان يتبادر الى أذهاننا سؤال ...كيف يتغير موقع الجسم
المتحرك بتسارع منتظم ؟
انظر الى البيانات الموجودة في الجدول التالي والتي تبين بيانات
الموقع عند فترات زمنية مختلفة لسيارة تتحرك بتسارع منتظم :
من خلال تمثيل الرسم البياني للبيانات السابقة يتضح أن حركة السيارة
غير منتظمة , فإزاحة الجسم تزداد خلال الفترة الزمنية .انظر للرسم البياني التالي
:
الميل الممثل في الشكل السابق يطابق السرعة المتجهة الممثلة بيانيا في الشكل
3-10 a
·
نلاحظ انه لا يمكننا عمل منحنى جيد
لـ(الموقع – الزمن ) باستخدام منحنى ( السرعة المتجهة – الزمن ) , وذلك لأن منحى ( السرعة المتجهة – الزمن ) لا يحتوي على أي معلومات حول موقع الجسم .ولكنه يحوي
معلومات عن إزاحته والتي يمكن ايجادها حاصل ضرب السرعة المتجهة في الزمن .
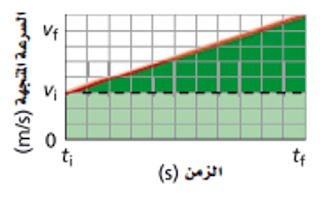
· الشكل التالي يوضح منحنى ( السرعة المتجهة –
الزمن ) لجسم يتحرك بسرعة منتظمة .
وبدارسة الشكل تحت
الخط البياني للمنحنى (المستطيل باللون الأخضر ) نجد أن سرعة الجسم V تمثل طول المستطيل , بينما الفترة الزمنية لحركة الجسم t تمثل
عرض المستطيل .
مما لا شك فيه اننا
نعلم انه ببساطة لحساب مساحة المستطيل فإننا نوجد حاصل ضرب الطول في العرض
·
يمكن إيجاد الإزاحة من منحنى ( السرعة المتجهة – الزمن ) لجسم يتحرك
بتسارع منتظم مبتدئا بسرعة ابتدائية vi وذلك بحساب المساحة تحت
المنحنى .
·
تحسب الإزاحة بتقسيم المساحة تحت المنحنى إلى مستطيل ومثلث
كما في
الشكل التالي :
-
لإيجاد مساحة المستطيل نستخدم القانون التالي :
-
لإيجاد مساحة المثلث نستخدم القانون التالي :
وكما عرفنا
سابقا فيمكن إيجاد الازاحة ∆d
من منحنى (السرعة المتجهة – الزمن ) وذلك حيث
وهذا يظهر لنا العلاقة بين السرعة المتجهة
والازاحة .ولا ننسى انه يجب ان يكون التسارع ثابتا .
كما يلي :
لذا يمكننا القول أن
المساحة الكلية تحت المنحى تساوي
بهذا القانون نستطيع إيجاد
الموقع بدلالة التسارع المتوسط .
·
يمكن ربط الموقع والسرعة والتسارع المنتظم في علاقة لا تتضمن الفترة
الزمنية .
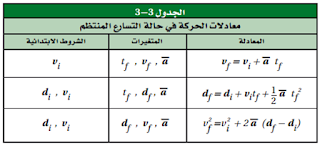
ويمكن تلخيص
المعادلات الثلاثة للحركة بتسارع ثابت كما في الجدول التالي:
·
الوسائل المستخدمة في مسائل
الحركة في بعد واحد:
1) المخططات التوضيحية للحركة.
2) الرسوم البيانية.
3) المعادلات الرياضية.
تم بحمد الله
نستقبل أسئلتكم واستفساراتكم واقتراحاتكم في خانة التعليقات
" نرد على جميع التعليقات "
بالتوفيق للجميع ...^_^

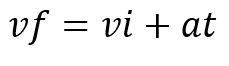


























في الازاحة هل اخذ بعين الاعتبار التغير الحادث في الحركة؟ أي هل أقوم بوضع ال - اذا كامت الحركة للخلف مثلاً؟ ام انني اقوم بوضع الكمية الكبيرة ناقص الصغيرة مقسومةً على الزمن فقط؟
ردحذففي سؤال:- تأكدي من صحة المعادلة التالية.
ردحذفV=(تربيع)r/a
noot saad :
ردحذفتمت الاجابة على سؤالك في الرابط التالي .... بالتوفيق ^_^
http://al-3lmnoor.blogspot.com/2016/11/blog-post_12.html