حل تمارين درس 1-1 التبرير الاستقرائي والتخمين - التبرير والبرهان

 

اكتب تخمينا يصف النمط في كل متتابعة مما يأتي، ثم استعمله لإيجاد الحد التالي في كل منها:

       1)   التكلفة: 4.50 ريالات، 6.75 ريالات، 9.00 ريالات، .....

الحل:

تزيد التكلفة كل مرة بمقدار 2.25 ريال عن المرة السابقة، وعليه فإن الحد التالي هو 11.25 ريالا.

 

       2)   مواعيد انطلاق الحافلات: 10:15 صباحا، 11:00 صباحا، 11:45 صباحا، ......

الحل:

يأتي كل موعد بعد 45 دقيقة من الموعد السابق له، و عليه فإن الموعد التالي هو 12:30 مساء.

 

       3)  

الحل:

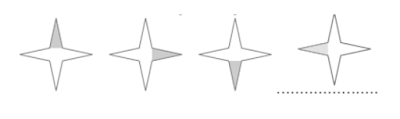
ينتقل التظليل إلى الجزء التالي كل مرة في اتجاه عقارب الساعة.

 

        4)  

الحل:

كل شكل في النمط يحوي دائرة إضافية خارجية زيادة على دوائر الشكل السابق.

 

       5)   3,3,6,9,15,……..

الحل:

كل حد في هذا النمط يساوي مجموع الحدين السابقين له ، وعليه فإن الحد التالي هو 24.

 

       6)   2,6,14,30,62,……….

الحل:

يزيد كل حد بمقدار 2 على مثلي الحد الذي يسبقه، وعليه فإن الحد التالي هو 126.

ضع تخمينا لكل قيمة أو علاقة هندسية مما يأتي:

      7)   ناتج ضرب عددين زوجيين.

الحل:

ناتج ضرب عددين زوجيين هو عدد زوجي. أمثلة : 

2x 4 = 8  ,  2 x 6 = 12  ,  4 x 8 = 32

 

     8)   العلاقة بين العددين a وb إذا كان a + b = 0.

الحل:

كل من a وb معكوس للآخر. أمثلة: 

2-2 =0 , -4+4 =0 , 8-8=0

 

     9)   العلاقة بين مجموعة النقاط في المستوى التي تبعد المسافة نفسها عن نقطة A.

الحل:

مجموعة النقاط في المستوى التي تبعد البعد نفسه عن النقطة ِA تكون دائرة.

 

    10)                  العلاقة بين APوPB إذا كانت M نقطة منتصف AB والنقطة P نقطة منتصف AM.

الحل:

طول PB يساوي ثلاثة أمثال   طول AP.

 

    11)                  إنتاج مصنع : استعمل الجدول المجاور الذي يبين عدد القطع المنتجة في مصنع لبعض السنوات.

عدد القطع المنتجة في مصنع لبعض السنوات

a)   أنشئ التمثيل البياني الأنسب لعرض هذه البيانات.

b)   ضع تخمينا لعدد القطع في سنة 2022 م.

     الحل :

            a)  

عدد القطع المنتجة في مصنع لبعض السنوات

            b)       سيكون عدد القطع في عام 2022 نحو 35 مليون تقريبا.

عدد القطع في عام 2022

 

 

أعط مثالا مضادا يبين أن كلا من التخمينات الآتية خاطئة.

      12)                  إذا كانت <A و <B متتامتين ، فإن لهما ضلعا مشتركا.

الحل:

في الشكل التالي <A و<B متتامتين ولكن لا يوجد لهما ضلع مشترك. 

      13)                  إذا قطع نصف مستقيم قطعة مستقيمة عند منتصفها ،فإنه يعامدها.

الحل:

في الشكل التالي يقطع نصف المستقيم القطعة المستقيمة عند منتصفها ولكنه لا يعامدها. 

 

اكتب تخمينا يصف النمط في كل متتابعة مما يأتي، ثم استعمله لإيجاد الحد التالي في كل منها.

        14)                  0, 2, 4, 6, 8

الحل:

كل حد في هذا النمط يزيد بمقدار 2 على الحد الذي يسبقه ،وعليه فإن الحد التالي هو 10 .

        15)                  3, 6, 9, 12, 15

الحل:

كل حد في هذا النمط يزيد بمقدار 3 على الحد الذي يسبقه ،و عليه فإن الحد التالي هو 18 .

        16)                  4, 8, 12, 16, 20

الحل:

كل حد في هذا النمط يزيد بمقدار 4 على الحد الذي يسبقه ، وعليه فإن الحد التالي هو 24 .

        17)                  2, 22, 222, 2222

الحل:

كل حد في هذا النمط يحتوي على الرقم 2 زيادة على أرقام الحد السابق له، وعليه فإن الحد التالي هو 22222 .

        18)                  1, 4, 9, 16

الحل:

ينتج كل حد عن تربيع العدد الطبيعي الذي يمثل ترتيبه، وعليه فإن الحد التالي هو  25

        19)                  1, 1/2 ,1/4 , 1/8  

الحل :

كل حد يساوي نصف الحد الذي يسبقه ، وعليه فإن الحد التالي هو 1/16 .

        20)                  مواعيد الوصول : 10:00 صباحا ، 12:30 مساء، 3:00 مساء ، .........

الحل:

يأتي كل موعد بعد ساعتين ونصف من الموعد الذي يسبقه ،وعليه فإن الموعد التالي هو 5:30 مساء.

       21)                  النسبة المئوية للرطوبة : ..........، 86% ،93% ،100%

الحل: تقل كل نسبة مئوية من النسبة السابقة بمقدار 7% ، وعليه فإن الحد التالي هو 79%.

       22)                  أيام العمل: الأحد، الثلاثاء، الخميس، ........

الحل: يأتي كل يوم عمل بعد يومين من يوم العمل السابق ، وعليه فإن الحد التالي هو  السبت.

       23)                  اجتماعات النادي : المحرم ، ربيع أول ، جمادى الأولى، .......

الحل : يعقد كل اجتماع بعد شهرين من الاجتماع السابق ، وعليه فإن الحد التالي هو رجب.

       24)                 

الحل:

اتجاه السهم في النمط يدور في اجاه عقارب الساعة من الشكل إلى الشكل الذي يليه.

 

        25)                

الحل:

يتحرك الجزء المظلل في كل شكل إلى المنطقة التالية من الشكل عكس اتجاه حركة عقارب الساعة.

      26)                

الحل:

 

       27)                 

  

الحل:

المثلث السفلي المظلل يتحرك في الجهة العليا اليمنى من الشكل الأول في اتجاه حركة عقارب الساعة، ويمر خلال كل مجموعة من المثلثات من شكل إلى الذي يليه. 

      28)                  رياضة : بدأ ماجد تمارين الجري السريع قبل خمسة أيام. فركض في اليوم الأول 0.5 km. وفي الأيام الثلاثة التالية 1.25km ، 1km ، 0.75 km . إذا استمر تمرينه على النمط ، فما المسافة التي يقطعها في اليوم السابع؟

الحل:

اليوم الأول = 0.5 km

اليوم الثاني = 0.75 km

اليوم الثالث = 1 km

اليوم الرابع = 1.25 km

اليوم الخامس = 1.5 km

اليوم السادس = 1.75 km

اليوم السابع = 2 km

 

ضع تخمينا لكل قيمة أو علاقة هندسية مما يأتي:

      29)                  ناتج ضرب عددين فرديين.

الحل:

ناتج ضرب عددين فرديين هو عدد فردي. أمثلة: 

1x3 = 3   ,   3x5 = 15    ,    5x7 = 37 

       

      30)                  ناتج ضرب عدد في اثنين، مضافا إليه واحد.

الحل:

ناتج ضرب عدد في اثنين، مضافا إليه واحد هو عدد فردي. أمثلة : 

3x2) +1 = 7    ,    (6x2) +1 = 13    ,   (7x2) +1 = 15) 

      31)                  العلاقة بين العددين a و b ، إذا كان ab=1 .

الحل:

2x (1/2) =1 , 5x (1/5) = 1 , 7x (1/7) = 1 

كل منهما مقلوب للآخر.

      32)                  العلاقة بين AB و مجموعة النقاط التي تبعد مسافات متساوية عن A و B.

الحل:

 مجموعة النقاط التي تبعد مسافات متساوية عن A و Bتشكل العمود المنصف لـ AB.

      33)                  العلاقة بين حجم المنشور وحجم الهرم اللذين لهما القاعدة نفسها والارتفاع نفسه.

الحل:

حجم المنشور يساوي 3 أمثال حجم الهرم.

      34)                  مدارس: يبين الجدول المجاور عدد الطلاب في إحدى المدرس الثانوية خلال الفترة من 1435هـ إلى 1438هـ. 

عدد الطلاب في إحدى المدارس الثانوية 1435هـ - 1438 هـ 

a)   أنشئ التمثيل البياني الأنسب لعرض هذه البيانات.

b)   ضع تخمينا معتمدا على بيانات الجدول ، واشرح كيف يؤيد تمثيلك البياني هذا التخمين.

   الحل:

         a)  

    

      b)    سيزداد عدد طلاب المدرسة في السنوات اللاحقة، ويظهر ذلك بوضوح من تزايد ارتفاع النقاط الذي يمثل عدد الطلاب في التمثيل البياني.

حدد ما إذا كان أي من التخمينات الآتية صحيحا أو خاطئا ، وإذا كان التخمين خاطئا ، فأعط مثالا مضادا.

     35)                  إذا كان n عددا أوليا ، فإن n+1 ليس أوليا .

الحل :

خاطئ ، إذا كان n=2 فإن التخمين خاطئ لأن n+1 = 3 ، و3 عدد أولي.

     36)                  إذا كان x عددا صحيحا ، فإن -x عدد موجب .

الحل :

خاطئ ، إذا كان x=2 ،فإن -x =-2 . و 2- عدد سالب. 

     37)                  في المثلث ABC إذا كان: (AB)² +(BC)² = (AC)² ، فإن المثلث ABC قائم الزاوية.

الحل:

صحيح. حسب نظرية فيثاغورس.

      38)                  إذا كانت مساحة مستطيل تساوي 20 m²، فإن طوله يساوي 10 m، وعرضه 2m.

الحل:

خاطئ ، يمكن أن يكون الطول 5m والعرض 4m.

      39)              سكان: استعمل الجدول أدناه لتعطي مثالا مضادا لكل من العبارتين الآتيتين:

a)   النسبة المئوية لمجموع عدد سكان المناطق الإدارية الأربع الواردة في الجدول أقل من 25% من سكان المملكة العربية السعودية.

b)   يزيد عدد سكان أي من المناطق الإدارية الأربع على ثلاثة ملايين نسمة.

الحل:

      a)   النسبة المئوية لعدد السكان في منطقة مكة المكرمة وحده يساوي 26% من سكان المملكة العربية السعودية.

     b)   عدد سكان منطقة المدينة المنورة 2.2 مليون نسمة.

 

      40)                  تخمين جولدباخ : ينص تخمين جولدباخ على أنه يمكن كتابة أي عدد زوجي أكبر من 2 على صورة مجموع عددين أوليين. فعلى سبيل المثال : 4=2+2, 6=3+3, 8=3+5.

a)   أثبت أن التخمين صحيح للأعداد الزوجية من 10 إلى 20.

b)   إذا أعطيت التخمين الآتي: يمكن كتابة أي عدد فردي أكبر من 2 على صورة مجموع عددين أوليين. فهل التخمين صحيح أم خاطئ؟ إذا كان خاطئا ، فأعط مثالا مضادا.

   الحل:

       a)   10=5+5, 12=5+7, 14=7+7, 16=5+11, 18=7+11, 20=7+13

       b)   خاطئ ، لا يمكن كتابة العدد 3 على صورة مجموع عددين أوليين. لأن 1+2 =3 ، حيث العدد 1 غير أولي. 

 

       41)                  هندسة: النقطتان الواقعتان على مستقيم تشكلان قطعة مستقيمة ، مثل AB. إذا أضيفت نقطة أخرى C على القطعة المستقيمة AB ، فإن النقاط الثلاث تشكل ثلاث قطع مستقيمة.

a)   ما عدد القطع المستقيمة المختلفة التي تتشكل من أربع نقاط على مستقيم ؟ ومن 5 نقاط على مستقيم؟

b)   ضع تخمينا لعدد القطع المستقيمة المختلفة التي تتشكل من n نقطة على مستقيم.

c)    اختبر تخمينك بإيجاد عدد القطع المستقيمة المختلفة التي تتشكل من 6 نقاط.

   الحل:

      a)  عدد القطع  المستقيمة التي تتشكل من أربع نقاط على مستقيم واحد هو ستة قطع مستقيمة. 

        عدد القطع المستقيمة التي تتشكل من خمس نقاط هو 10 قطع مستقيمة. 

      

      b)   عدد القطع المستقيمة يساوي مجموع الأعداد الطبيعية الأقل من n.

      c)    تتكون 15 قطعة مستقيمة. فالتخمين صحيح. 

     42)                  اكتشف الخطأ : يتناقش أحمد وعلي في موضوع الأعداد الأولية. فيقول احمد : إن جميع الأعداد الأولية أعداد فردية. في حين يقول علي: ليست جميع الأعداد الأولية فردية. هل قول أي منهما صحيح؟ فسر إجابتك.

الحل:

قول علي صحيح، لأن العدد 2 عدد أولي زوجي.

 

      43)                  مسالة مفتوحة : اكتب متتابعة عددية تتبع حدودها نمطين مختلفين ، ووضح النمطين.

الحل:

2,4,16,256,65536. يمكن إيجاد كل حد بتربيع الحد السابق له ، كما يمكن إيجاد كل حد باستعمال الصيغة 2^2n-1 ، حيث n>=1.

      44)                  تبرير : تأمل التخمين : "إذا كانت نقطتان تبتعدان المسافة نفسها عن نقطة ثالثة معلومة ، فإن النقاط الثلاث تقع على استقامة واحدة" . هل هذا التخمين صحيح أم خاطئ؟ وإذا كان خاطئا فأعط مثالا مضادا.

الحل: خطئ ، إذا كونت النقاط زاوية مستقيمة يكون التخمين صحيحا، أما إذا لم تكن النقاط الثلاث على استقامة واحدة ، فيكون التخمين خطئا.

 

       45)                  اكتب: افترض أنك تجري مسحا. اختر موضوعا واكتب ثلاثة أسئلة يتضمنها مسحك. كيف تستعمل التبرير الاستقرائي مع البيانات التي تحصل عليها من خلال هذا المسح؟

الحل:

أود أن أجري مسحا لأنواع الأنشطة التي يمارسها الناس في عطلة الأسبوع، وأطرح الأسئلة الآتية: ما عمرك؟ ما نوع النشاط الذي تفضل ممارسته في عطلة نهاية الأسبوع؟ ما مدى مواظبتك على ممارسة هذا النشاط؟ ثم بعد ذلك أستعمل التبرير الاستقرائي لإيجاد أنماط في الإجابات لتحديد ما إذا كان الأشخاص المتساوون في العمر يفضلون ممارسة الأنشطة نفسها أم لا.

 

       46)               انظر إلى النمط الآتي:

 

ما الشكل التالي في النمط؟

 

الحل:

B. (كل شكل في النمط ينقص عدد أضلاعه ضلعا واحدا عما قبله. )

 

      47)                  إذا علمت أن a=10, b=1 ، فما قيمة العبارة الآتية؟

2b+ab\(a + b)

الحل:

2(1)+(10)(1)\(10 + 1) = 32\11

 

      48)                  في الشكل المجاور، ABمحور تناظر <DAC. أي الاستنتاجات الآتية ليس صحيحا بالضرورة؟

a)   <DAB =BAC.

b)   <DAC زاوية قائمة.

c)    A و D على استقامة واحدة

d)   2(m<BAC) = m<DAC

      الحل:

B.

      49)                  أحواض سمك: اشترى باسم حوض سمك صغير على شكل أسطوانة دائرية قائمة، طول قطر قاعدتها 25 cm، و ارتفاعها 35 cm، أوجد حجم الماء اللازم لملء الحوض.

الحل:

حجم الأسطوانة = باي X نصف القطر² x الارتفاع

                 17180.6 cm³ = 3.14 x 12.5² x35

أوجد محيط المثلث ABC إذا أعطيت إحداثيات رؤوسه في كل مما يأتي:

      

      50)                  A(1,6), B(1,2), C(3,2)

الحل:

 

من خلال رسم المثلث ABC السابق نجد أن :

طول AB = 4 cm

طول BC = 2 cm

لإيجاد طول AC نستخدم نظرية فيثاغورس

      51)                  A(-3,2) , B(2,9) ,C(0,10)

الحل:

 

 

توضيح: بما أن المثلث غير قائم الزاوية فإننا لا نستطيع تطبيق نظرية فيثاغورس بشكل مباشر وبما أن أطوال أضلاع المثلث غير معلومة فإننا سنحتاج لـ:

        -       تقسيم الشكل إلى مثلثات تشكل زاوية قائمة ومن ثم سنقوم بتطبيق نظرية فيثاغورس على كل جزء وذلك بهدف إيجاد أطوال الأضلاع للمثلث.

        -       حساب محيط المثلث والذي يساوي مجموع أطوال الأضلاع.

 

-       تقسم الشكل إلى مثلثات قائمة الزوايا لإيجاد أطوال الأضلاع.

1)   المثلث الأول يشكل زاوية قائمة مع محور Y مما يسهل علينا إيجاد طول الضلع AC. كما هو موضح في الشكل التالي باللون الأخضر.

 

سنقوم باستخدام نظرية فيثاغورس هنا بما أن المثلث المتشكل أمامنا قائم الزاوية ومن خلال الرسم فإن طول الضلع AC يساوي

2)   المثلث الثاني وهو مثلث قائم الزاوية يوضح الأضلاع المكونة للزاوية القائمة والتي سنقوم باستخدامها لإيجاد طول الضلع AB.

 

من خلال استخدام نظرية فيثاغورس نجد أن طول الضلع AB يساوي

3)   المثلث الثالث وهو مثلث قائم الزاوية يوضح الأضلاع المكونة للزاوية القائمة والتي سنقوم باستخدامها لإيجاد طول الضلع BC.

من خلال استخدام نظرية فيثاغورس نجد أن طول الضلع BC يساوي

          -       حساب محيط المثلث:

        52)                  جبر: قياس زاويتين يساوي (16z -9)⁰  و (4z +3)⁰ . أوجد قياس كل منهما.

الحل:

بما أن الزاويتين متتامتان فهذا يعني أن مجموعهما يساوي 90⁰

نعوض عن قيمة z في المعادلتين لإيجاد قيمة كل زاوية :

الزاوية الأولى:

الزاوية الثانية:

         53)                  جبر: إذا علمت أن: z=-5 , y=-4, x=3 ، فأوجد قيمة 5|x+y|-3|2-z|

الحل:

جبر: اكتب كلمة "صح" بجوار العبارة الصحيحة وكلمة " خطأ " بجوار العبارة الخاطئة.

 

       54)                  كل مربع هو مستطيل

الحل: صح

 

       55)                  5-2x3=9

الحل: خطأ، لأن 

 5-2x3 =5-6 =-1 

       56)                  العدد 9 عدد أولي

الحل: خطأ، لأن العدد 9 يقبل القسمة على 3، فهو عدد أولي.