حل تحقق من فهمك لدرس 6-1 البرهان الجبري - التبرير والبرهان

 

تحقق من فهمك:

اذكر الخاصية التي تبرر كلا من العبارتين الآتيتين:

1A) إذا كانت 4x+(-5)=-1، فإن x+4+(-5)=x-1

الحل:

خاصية الجمع للمساواة.

1B) إذا كانت 5=y، فإن y=5.

الحل:

خاصية التماثل للمساواة.

1C) أثبت أنه إذا كان 2x-13=-5، فإن x=4. اكتب تبريرا لكل خطوة.

الحل:

2x-13=-5                        ( معطيات)

2x-13+13=-5+13      ( خاصية الجمع للمساواة)

 2x=8                              (بالتبسيط)

X=4                         (خاصية القسمة للمساواة)

 

اكتب برهانا ذا عمودين لإثبات صحة كل من التخمينين الآتيين:

2A) إذا كان 5x+1 /2 -8=0 ، x=3.

الحل:

المعطيات: 5x+1 / 2 -8= 0

المطلوب: x=3

البرهان:

العبارات		المبررات
5x+1 /2 =0	1	المعطيات
5x+1 /2 = 8	2	خاصية الجمع للمساواة
2(5x+1/2) =2(8)	3	خاصية الضرب للمساواة
5x+1=16	4	التبسيط
5x=15	5	خاصية الطرح للمساواة
x=3	6	خاصية القسمة للمساواة

 

 

2B) فيزياء: إذا كانت المسافة d التي يقطعها جسم متحرك بسرعة ابتدائية u وسرعة نهائية في زمن t تعطى بالعلاقة d=t*(u+v/2) ، فغن u=2d/t -v.

الحل:

المعطيات: d=t.(u+v/2)

المطلوب: u=(2d/t)-v

البرهان:

العبارات	المبررات
D=t.(u+v/2)	معطيات
d/t =u+v/2	خاصية القسمة للمساواة
2(d/t)=2(u+v/2)	خاصية الضرب للمساواة
2d/t =u+v	بالتبسيط
2d/t – v =u	خاصية الطرح للمساواة
U=2d/t -v	خاصية التماثل للمساواة

 

اكتب برهانا ذا عمودين، لإثبات صحة كل من التخمين الآتيين:

3A) إذا كان m<A=37⁰ ، <A=<B، فإن m<B=37⁰.

الحل:

المعطيات: <A=<B و m<A=37.

المطلوب: m<B=37

البرهان:

العبارات	المبررات
<A=<B و m<A=m<B	معطيات
m<A=m<B	تعريف تطابق الزوايا
370 = m<B	خاصية التعويض للمساواة
m<B=370	خاصية التماثل

 

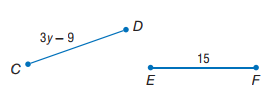
3B) إذا كان CD=EF، فإن y=8.

الحل:

المعطيات: CD=EF

CD=3y-9,EF=15

المطلوب: y=8.

البرهان:

العبارات	المبررات
CD=EF	معطيات
CD=EF	تعريف تطابق القطع المستقيمة
3y-9=15	خاصية التعويض للمساواة
3y=24	خاصية الجمع للمساواة
Y=8	خاصية القسمة للمساواة