حل تمارين درس 6-1 البرهان الجبري - التبرير والبرهان

 

تأكد:

اذكر الخاصية التي تبرر العبارة:

       1)  إذا كان 5=x، فإن x=5.

الحل:

خاصية التماثل للمساواة.

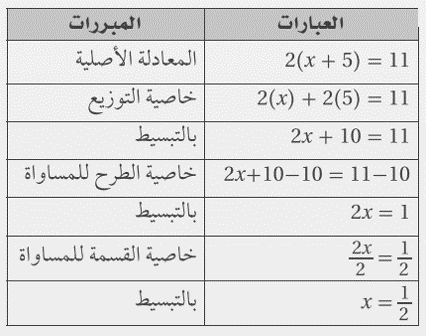
       2)  أثبت أنه إذا كان 2(x+5)=11، فإن x=1/2 اكتب تبريرا لكل خطوة.

الحل:

      3)  أكمل البرهان الآتي:

المعطيات: y+2/3 =3

المطلوب: y=7

البرهان:

الحل:

برهان: اكتب برهانا ذا عمودين لإثبات صحة كل من التخمينين الآتيين:

      4)  إذا كان -4(x-3)+5x=24، فإن x=12.

الحل:

المعطيات:

-4(x-3)+5x=24

المطلوب: x=12.

البرهان:

 

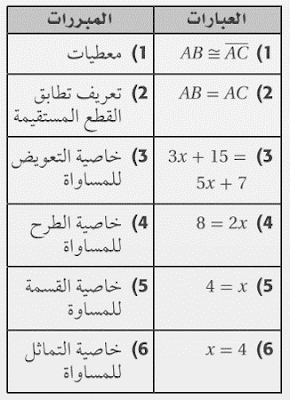
      5)  إذا كان AB=CD، فإن x=7.

الحل:

المعطيات: AB=CD

المطلوب:

x=7

البرهان:

 

       6)  صحة: يراقب بدر معدل نبضات قلبه في الدقيقة الواحدة مستعملا جهاز قياس النبض، ليتحقق من أنه يقع ضمن المدى الطبيعي. ويمكن تقدير هذا المعدل باستعمال الصيغة T=0.75(200-a)، حيث T معدل نبضات القلب، و a عمر الشخص.

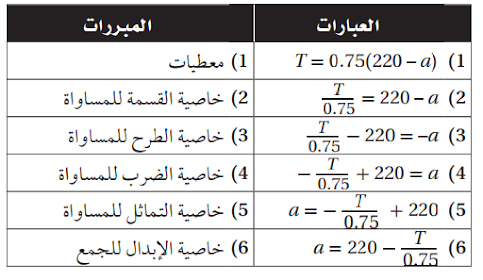
a)  أثبت أنه إذا علمت معدل نبضات قلب شخص، فإنه يمكنك حساب عمره مستعملا الصيغة: a=220-T/0.75.

الحل:

b)  إذا كان معدل نبضات قلب بدر يساوي 153، فكم يكون عمره؟ ما الخاصية التي تؤكد صحة حساباتك؟

الحل:

عمره 16 سنة، خاصية التعويض للمساواة.

 

تدرب وحل المسائل:

اذكر الخاصية التي تبرر كل عبارة مما يأتي:

       7)  إذا كان a+10=20، فإن a=10.

الحل:

خاصية الطرح للمساواة.

       8)  إذا كان x/3=-15، فإن x=-45.

الحل:

    خاصية الضرب للمساواة.

       9)  إذا كان 5(x+7)=-3، فإن 5x+35=-3.

الحل:

خاصية التوزيع.

      10)                 إذا كان 3(x-2/3)=4، فإن 3x-2=4

الحل:

خاصية التوزيع.

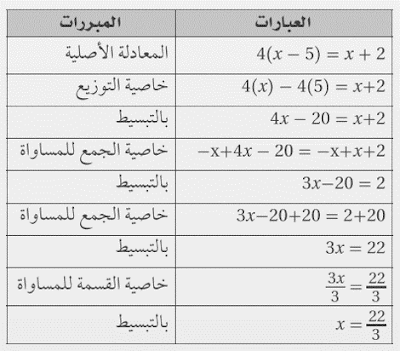
      11)                 أثبت أنه إذا كان 4(x-5)=x+2 فإن x=22/3 مبررا كل خطوة.

الحل:

اذكر الخاصية التي تبرر كل عبارة مما يأتي:

     12)                 إذا كان m<1=m<2,m<2=m<3، فإن m<1=m<3.

الحل:

خاصية التعدي للمساواة.

     13)                 XY=XY

الحل:

خاصية الانعكاس للمساواة.

     14)                 إذا كان 1/5BC=1/5DE، فإن BC=DE.

الحل:

خاصية الضرب للمساواة.

     15)       إذا كان m<2=25، m<1=25،فإن m<1=m<2.

الحل:

خاصية التعويض للمساواة.

16)     إذا كان BC=CD، ِ AB=BC،فإن AB=CD.

الحل:

خاصية التعدي للمساواة.

أكمل البرهانين الآتيين:

    17)       العطيات: 8-3x/4 =32

المطلوب: x=-40

البرهان:

الحل:

 

      18)                 علوم: تعطى المسافة d التي يقطعها جسم متحرك بالقدم بالصيغة: d=vt+1/2 at²، حيث v سرعة الجسم بالقدم لكل ثانية، و t الزمن بالثانية، وa التسارع بالقدم لكل ثانية تربيع.

اكتب برهانا ذا عمودين، لإثبات أن التسارع يمكن أن يحسب بالصيغة a=2d-2vt/t² .

الحل:

 

برهان: اكتب برهانا ذا عمودين لإثبات صحة كل من التخمينين الآتيين:

       19)                 إذا كان -1/3 n=12،فإن n=-36.

الحل:

المعطيات: -1/3n=12

المطلوب: n=-36

البرهان:

 

      20)                 إذا كان -3r+1/2=4،فإن r=-7/6.

الحل:

المعطيات: -3r+1/2 =4

المطلوب: r=-7/6

البرهان:

 

      21)                 علوم: يعطى قانون الغاز المثالي بالصيغة PV=nRT، حيث P: الضغط بوحدة الضغط الجوي(atm)  ، و V: الحجم باللترات، و n: عدد مولات الغاز، R: ثابت الغاز المثالي، حيث R=0.0821، T: درجة الحرارة بالكلفن.

a)  أثبت أنه إذا كان ضغط الغاز وحجمه وعدد مولاته جميعها معلومة، فإنه يمكن حساب درجة حرارته باستعمال الصيغة T=PV/nR.

الحل:

المعطيات:

R=0.0821,PV=nRT

المطلوب: T=PV/nR

البرهان:

 

b)  ما درجة حرارة 1 مول من الأكسجين موجود في إناء سعته 25L ، وتحت ضغط مقداره 1atm؟ ما الخاصية التي تبرر حساباتك؟

الحل:

305 درجات كلفن تقريبا، خاصية التعويض للمساواة.

برهان: اكتب برهانا ذا عامودين لإثبات صحة كل من التخمينات الآتية:

      22)               إذا كانت DF=EG، فإن x=10.

الحل:

المعطيات: DF=EG

المطلوب: x=10

البرهان:

 

       23)               إذا كانت AB=AC، فإن x=4.

الحل:

المعطيات: AB=AC

المطلوب: x=4

البرهان:

 

        24)               إذا كانت <Y=<Z، فإن x=100.

 

الحل:

المعطيات: <Y=<Z

المطلوب: x=100

البرهان:

 

        25)               إذا كانت <MPN=<QPN، فإن x=16.

الحل:

المعطيات: <MPN=<QPN

المطلوب: x=16

البرهان:

  

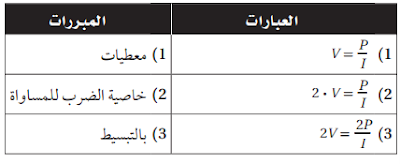
      26)                 كهرباء: يمكن حساب فرق الجهد V للدائرة الكهربائية باستعمال القانون V=P/I، حيث P: القدرة الكهربائية، و I شدة التيار الكهربائي المار في الدائرة.

a)  اكتب برهانا لإثبات أنه عندما تكون القدرة الكهربائية ثابتة، فإن فرق الجهد يصبح نصف ما كان عليه عندما تتضاعف شدة التيار الكهربائي.

الحل:

المعطيات: V=P/I

المطلوب: V/2 =P/2I

البرهان:

b)  اكتب برهانا لإثبات أنه عندما تكون شدة التيار الكهربائي ثابتة، فإن فرق الجهد يتضاعف عندما تتضاعف القدرة الكهربائية.

الحل:

المعطيات: v=P/I

المطلوب: 2V=2P/I

البرهان:

        27)                 تمثيلات متعددة: افترض أن مكعبا طول ضلعه s وحدة.

a)  حسيا: ارسم أو اعمل نماذج لمكعبات أطوال أضلاعها 2,4,8,16 وحدة.

الحل:

b)  جدوليا: أوجد حجم كل مكعب نظم نتائجك في جدول مثل المجاور.

الحل:

طول الضلع (s)	الحجم (V)
2	8
4	64
8	512
16	4096

 

 

c)   لفظيا: استعمل الجدول لعمل تخمين حول تغير حجم المكعب عندما يتضاعف طول ضلعه. عبر عن تخمينك لفظيا.

الحل:

إذا تضاعف طول ضلع المكعب، فغن حجمه يصبح 8 أمثال الحجم الأصلي.

 

d)  جبريا: اكتب تخمينك على صورة معادلة جبرية.

الحل:

8V=(2s)³

 

e)  منطقيا: اكتب برهانا لتخمينك. تأكد من كتابة المعطيات والمطلوب في بداية البرهان.

الحل:

المعطيات: مكعب طول ضلعه s وحدة، وحجمه V وحدة مكعبة.

المطلوب: 8V=(2s)³

البرهان:

مسائل مهارات التفكير العليا:

       28)                 تحد: تقع النقطة P على AB. إذا علمت أن طول AP يساوي 2x+3، طول PB يساوي 3x+1/2، وطول AB يساوي 10.5 وحدات، فارسم شكلا يوضح المسألة، و أثبت أن طول AP يساوي ثلثي طول AB.

الحل:

المعطيات:

 AP=2x+3

AB=10.5

المطلوب:

AP=2/3 AB

البرهان:

تبرير: صف الجمل الآتية إلى صحيحة أحيانا أو صحيحة دائما أو غير صحيحة أبدا. فسر تبريرك.

      29)                 إذا كان a و b عددين حقيقين، وكان a+b=0، فإن a=-b.

الحل:

صائبة دائما، إذا كان a+b=0 فإن a+b-b=0-b ( خاصية الطرح للمساواة) إذن a=-b (بالتبسيط) ، ولذا تكون هذه العبارة صائبة دائما.

 

      30)                 إذا كان a و b عددين حقيقين، وكان a²=b  فإن a=√b.

الحل:

صائبة أحيانا، إذا كانت a=1 فإن a2=1=b إذن √ b = √1 = 1 = a فتكون الجملة صائبة. أما إذا كانت a=-1، فإن a2=(-1)2=1=b ويكون √ b= √ 1 = 1 ≠ a وبذلك تكون الجملة غير صائبة.

 

      31)                 تحد: وضعت آمنة تخمينا ينص على أن مجموع أي عددين صحيحين فريدين هو عدد زوجي.

a)  أعط أمثلة تؤيد هذا التخمين، ثم فسر لماذا لا تثبت هذه الأمثلة صحة التخمين.

الحل:

3+3=6، 7+9=16،5+7=12. هذه أمثلة توضح التخمين، ولكنها لا تثبته، وذلك لأن الأعداد الفردية المذكورة لا تمثل جميع الأعداد الفردية، إنما هي أمثلة فقط.

 

b)  يمكن كتابة العدد الفردي على الصورة 2n-1. أعط أمثلة تؤيد ذلك.

الحل:

3=2(2)-1, 7=2(4)-1, 5=2(3)-1

 

c)   ما العدد الذي تكون الأعداد الزوجية جميعها مضاعفات له؟ فسر لفظيا كيف يمكن استعمال إجابتك عن الفرعين a,b، لإثبات صحة تخمين آمنة.

الحل:

سوف أجمع العبارتين 2n-1 و 2m-1، اللتين تمثلان أي عددين فرديين، وأثبت أن المجموع من مضاعفات العدد 2.

 

d)  اكتب برهانا جبريا لإثبات أن مجموع أي عددين صحيحين فريدين هو عدد صحيح زوجي.

الحل:

افترض أن العددين الصحيحين الفرديين هما: 2n-1 و 2m-1، فيكون المجموع (2n-1)+(2m-1) يساوي 2n+2m-2. نلاحظ أن كل حد يحوي العامل 2، لذا يمكن إخراجه عاملا مشتركا لينتج 2(n+m-1). وهذه الصيغة هي مضاعف للعدد 2، إذن هي تمثل عددا زوجيا، لذا فإن مجموع عددين صحيحين فرديين هو عدد صحيح زوجي.

 

      32)                 اكتب: ما أوجه الشبه وأوجه الاختلافات بين البرهان الحر والبرهان ذي العامودين. أي البرهانين تجده أسهل للكتابة؟ برر إجابتك.

الحل:

البرهان الحر هو نوع من البراهين الذي تكتب فيه الخطوات جملا كاملة على شكل فقرة. وهذا النوع من البرهان يماثل في محتواه البرهان ذا العامودين، ولكنه يختلف عنه شكلا، ففي البرهان ذي العامودين تكتب العبارات في عمود، وتكتب المبررات في عمود آخر بجانب العمود الأول.

 

تدريب على اختبار

     33)               في الشكل أدناه: m<CFE=90⁰ و <AFB=<CFD.

أي مما يأتي ليس صحيحا بالضرورة؟

A m<BFD =m<BFD

B FC محور تناظر للشكل

C m<CFD =m<AFB

D <CFE قائمة

الحل:

B.

 

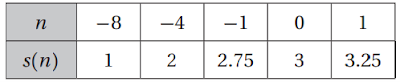
      34)                مراجعة: أي علاقة يمكن أن تستعمل لإيجاد قيم s(n) في الجدول التالي؟

A s(n)=-n+7

B s(n)=-2n+3

C s(n) =1/2n+5

D s(n)=1/4n +3

الحل:

D.

 

مراجعة تراكمية

حدد ما إذا كانت كل جملة مما يأتي صحيحة دائما أو صحيحة أحيانا أو غير صحيحة أبدا. فسر إجابتك.

     35)                 أي أربع نقاط تقع في المستوى نفسه.

الحل:

صحيحة أحيانا، لأن المستوى يتضمن ثلاث نقاط على الأقل، أما النقطة الرابعة فإما أن تقع على هذا المستوى وإما ان تقع على مستوى آخر.

 

     36)                 الزاويتان المنفرجتان متكاملتان

الحل:

غير صحيحة أبدا، مجموع الزاويتين المتكاملتين يساوي 180⁰.

إذن الزاويتين المنفرجتان لا يمكن أن تكونا متكاملتين.

 

     37)                 المستويان P وQ يتقاطعان في المستقيم m. والمستقيم m يقع في كلا المستويين P وQ.

الحل:

صحيحة دائما، بما أن المستقيم هو خط تقاطع المستويين، فإن هذا المستقيم يقع في كلا المستويين.

 

حدد ما إذا كانت النتيجة صائبة أم لا في كل مما يأتي، اعتمادا على العبارة التالية والمعطيات مبررا إجابتك. "يقبل العدد القسمة على 3 إذا كان يقبل القسمة على 6".

      38)                 المعطيات: 24 يقبل القسمة على 6.

النتيجة: 24 يقبل القسمة على 3.

الحل:

صحيحة، بما أن 24  تقبل القسمة على 6 ، إذن وفق قانون الفصل المنطقي، فإنها تقبل القسمة على 3.

      39)                 المعطيات: 27 يقبل القسمة على 3

النتيجة: 27 يقبل القسمة على 6.

الحل:

غير صحيحة، 27/6 = 4.5 والعدد 4.5 ليس عددا صحيحا.

 

      40)                 المعطيات: 85 لا يقبل القسمة على 3.

النتيجة: 85 لا يقبل القسمة على 6.

الحل:

صحيحة، بحسب المعاكس الإيجابي للعبارة وقانون الفصل المنطقي، إذا قبلت ال85 القسمة على 6 و6 تقبل القسمة على 3، إذن يجب أن تقبل 85 القسمة على 3، وهذا مخالف للمعطى ، إذن 85 لا تقبل القسمة على 6.

 

     41)                 مبان: توجد أربع بنايات في مدرسة، لا يوجد ثلاث منها على استقامة واحدة. ما عدد ممرات المشاة اللازمة لربط كل بنايتين بممر مشاة واحد؟

الحل:

6.

استعد للدرس اللاحق

أوجد طول كل قطعة مستقيمة مما يأتي مستعينا بالشكل.

     42)                 ST

الحل:

RT=RS+ST

ST=RT-RS

ST=4.0-1.2

ST=2.8 cm

     43)                 WX

 

الحل:

WY=WX+XY

WX=XY

WX=WY/2

WX=4.8/2

WX=2.4cm

     

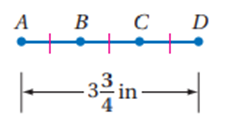
      44)                 BC

الحل:

3(3/4)in

10/4in

BC=5/4

BC=1(1/4)in