حل تمارين درس 1-2 المستقيمان المتوازيان والقاطع - التوازي والتعامد
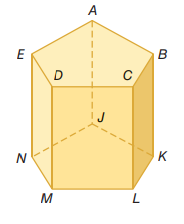
حدد كلا مما يأتي مستعملا متوازي المستطيلات في الشكل المجاور:
1)
جميع القطع المستقيمة التي
توازي SV.
الحل:
YX,YU,ZW.
2)
مستوى يوازي المستوى ZWX.
الحل:
TUV.
3)
قطعة مستقيمة تخالف TS وتحتوي على النقطة W.
الحل:
WZ,WU.
4)
إنشاءات: استعمل الشكل
المجاور لتحديد كل مما يأتي:
a) ثلاثة أزواج من المستويات المتوازية.
الحل:
المستوى ABCD يوازي المستوى FGHE ، المستوى ADEF يوازي المستوى BCHG ، المستوى DCHE يوازي المستوى ABGF.
b) ثلاث قطع مستقيمة توازي DE.
الحل:
GH,BG,AF.
c) قطعتين مستقيمتين متوازيتان FE.
الحل:
BC
و AD.
d) زوجين من القطع المستقيمة المتخالفة.
الحل:
JK وBG ، JK و CH.
مستعملا الشكل المجاور، صنف كل زوج من الزوايا فيما يأتي إلى زاويتين متبادلتين داخليا، أو متبادلتين خارجيا، أو متناظرتين، أو متحالفتين.
5) 1> و 8>
الحل:
متبادلتان خارجيا.
6) 2> و 4>
الحل:
متناظرتان.
7) 3> و 6>
الحل:
متبادلتان داخليا.
8) 6> و 7>
الحل:
متحالفتان.
استعمل الشكل المجاور لتحديد القاطع الذي يصل بين كل زوج من الزوايا فيما يأتي، ثم صنف زوج الزوايا إلى زاويتين متبادلتين داخليا، أو متبادلتين خارجيا، أو متناظرتين، أو متحالفتين:
9) <2 و<4
الحل:
المستقيم n، متناظرتان.
10) <5
و<6
الحل:
المستقيم P، متبادلتان خارجيا.
11) <4
و<7
الحل:
المستقيم m، متحالفتان.
12) <2
و<7
الحل:
المستقيم P، متبادلتان داخليا.
حدد كلا مما يأتي مستعملا الشكل المجاور:
13) جميع القطع المستقيمة التي توازي DM.
الحل:
CL,EN,BK,AJ
14) مستوى يوازي المستوى ACD.
الحل:
JLM.
15) قطعة مستقيمة تخالف BC.
الحل:
EN.
16) مستوى يتقاطع مع المستوى EDM.
الحل:
AEN, DCL, NML, AED
17) جميع القطع المستقيمة
التي تخالف AE.
الحل:
KL, CL, BK, ML, DM, NM, KJ
18) قطعة مستقيمة توازي EN.
الحل:
AJ.
19) قطعة مستقيمة توازي AB وتمر بالنقطة J.
الحل:
JK.
20) قطعة مستقيمة تخالف CL وتمر بالنقطة E.
الحل:
AE.
مستعملا الشكل المجاور، صنف كل زوج من الزوايا فيما يأتي إلى زاويتين متبادلتين داخليا، أو متبادلتين خارجيا، أو متناظرتين، أو متحالفتين.
21) <4
و <9
الحل:
متناظرتان.
22) <5
و <7
الحل:
متحالفتان.
23) <3
و <5
الحل:
متبادلتان داخليا.
24) <10 و <11
الحل:
متناظرتان.
25) <1
و <6
الحل:
متبادلتان خارجيا.
26) <6
و <8
الحل:
متبادلتان داخليا.
27) <2
و <3
الحل:
متحالفتان.
28) <9
و<10
الحل:
متبادلتان خارجيا.
29) <4
و <11
الحل:
متبادلتان خارجيا.
30) <7
و<11
الحل:
متبادلتان داخليا.
سلم طوارئ: استعمل صورة سلم الطوارئ المجاورة، لتحديد القاطع الذي يصل بين كل زوج من الزوايا فيما يأتي، ثم صنف زوج الزوايا إلى زاويتين متبادلتين داخليا، أو متبادلتين خارجيا، أو متناظرتين:
31) <1
و<3
الحل:
المستقيم a، متناظرتان.
32) <2
و<4
الحل:
المستقيم a، متحالفتان.
33) <4
و<5
الحل:
المستقيم c، متبادلتان داخليا.
34) <5
و<6
الحل:
المستقيم d، متبادلتان داخليا.
35) <7
و<8
الحل:
المستقيم d، متناظرتان.
36) <2
و<3
الحل:
المستقيم d، متبادلتان داخليا.
37) كهرباء: استعمل الصورة المجاورة في
فقرة الربط مع الحياة والمعلومات أدناها للإجابة عما يأتي:
a)
ماذا يجب أن تكون عليه العلاقة بين خطي التوصيل الكهربائي P و m؟ وضح إجابتك.
الحل:
بما أن
المستقيمين يقعان في المستوى نفسه و غير متلاقيين فإنهما متوازيان.
b)
ما العلاقة بين ذراع الحمل q و خطي التوصيل الكهربائي P وm؟
الحل:
الخط q يخالف كلا من P وm.
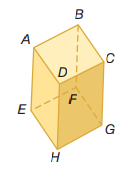
استعمل الشكل المجاور لتصف العلاقة بين كل زوج من القطع المستقيمة الآتية بكتابة:
متوازيتان، أو متخالفان، أو متقاطعتان:
38)FG
وBC
الحل:
متوازيان.
39)AB
وCG
الحل:
متخالفتان.
40) DH
وHG
الحل:
متقاطعتان.
41) DH
وBF
الحل:
متوازيتان.
42) EF
وBC
الحل:
متخالفتان.
43) CDوAD
الحل:
متقاطعتان.
44) خداع بصري: صمم نموذج الخداع البصري المجاور باستعمال مربعات متطابقة ومستقيمات فقط.
a)
ما العلاقة بين AB و CD؟
فسر تبريرك.
الحل:
AB||DC، المسافة بين القطعتين المستقيمتين هي نفسها
من أي موقع على القطعة المستقيمة.
b)
ما العلاقة بين MN و QR؟
وما العلاقة بين القطعتين المستقيمتين AB وCD
والقطعة المستقيمة OP؟
الحل:
MN||QR،OP قاطع لكل من CD و AB.
45) سلم كهربائي: يتكون السلم
الكهربائي من درجات مثبتة على مسار متصل بمحرك، حيث تطوى درجات أعلى السلم وأسفله،
ليتكون سطح مستو عند الدخول والخروج كما في الشكل التالي.
a)
ما العلاقة بين أسطح الدرجات الصاعدة؟
الحل:
أجزاء من
مستويات متوازية.
b)
ما العلاقة بين أسطح الدرجات الثلاث أعلى السلم؟
الحل:
تقع جميعها في
المستوى نفسه.
c)
ما العلاقة بين أسطح الدرجات الصاعدة و أسطح الدرجات الهابطة في مسار
السلم؟
الحل:
أي مستوى يحوي
سطح درجة صاعدة، يتقاطع مع أي مستوى يحوي سطح درجة هابطة.
مسائل مهارات التفكير العليا
46) مسألة مفتوحة: يحتوي المستوى P المستقيمين المتوازيين a,b.
ويقطع المستقيم c المستوى P عند النقطة J. إذا كان المستقيمان a,c متخالفين، والمستقيمان b,c
غير متخالفين، فارسم شكلا يمثل هذا الوصف.
الحل:
47) تحد افترض أن النقاط A,B,C تقع في المستوى P، و أن النقاط D,E,F تقع في المستوى Q. وأن المستقيم m يحتوي النقطتين D,F ولا يقطع المستوى P. وأن المستقيم n يحوي النقطتين A,E.
a) ارسم شكلا يمثل هذا الوصف.
الحل:
b)
ما العلاقة بين المستويين P وQ؟
الحل:
متوازيان.
c)
ما العلاقة بين المستقيمين m وn؟
الحل:
متخالفان.
تبرير: المستويان X و Y
متوازيان، والمستوى Z يقطع المستوى X.
والمستقيم AB
يقع في المستوى X،
والمستقيم CD
يقع في المستوى Y،
والمستقيم EF
يقع في المستوى Z.
حدد ما إذا كانت كل عبارة فيما يأتي صحيحة دائما، أو صحيحة أحيانا، أو غير صحيحة
أبدا. وضح إجابتك:
48) AB
يخالف CD.
الحل:
صحيحة أحيانا، إما أن تكون AB
موازيا لCD
أو يخالفه، لأنهما لا يتقاطعان أبدا، ولا يقعان في المستوى نفسه.
49) AB
يقطع EF.
الحل:
صحيحة أحيانا، لأن المستقيمين يمكن أن يكونا
متقاطعين أو متخالفين أو متوازيين.
50) اكتب: وضح لماذا لا يكون المستويان
متخالفين أبدا.
الحل:
لا يكون المستويان متخالفين، لأن تعريف المستقيمين المتخالفين ينص على أن المستقيمين لا يتقاطعان ولا يقعان في المستوى نفسه. أما في
المستويات فلا توجد إلا حالتين للمستويين، إما متوازيين أو متقاطعين.
تدريب على اختبار
51) أي مما يأتي يمثل زاويتن متبادلتين
خارجيا؟
a)
<1
و<5
b) <2 و<6
c) <2 و <10
d) <5 و <9
الحل:
B.
52) يمثل الشكل المجاور صندوق بريد. أي
مما يأتي يصف <1 و<2؟
a)
زاويتان متبادلتان خارجيا
b)
زاويتان متبادلتان داخليا
c)
زاويتان متحالفتان
d)
زاويتان متناظرتان
الحل:
D.
مراجعة تراكمية:
أوجد قياسات الزوايا في كل مما يأتي:
53) m<9=(2x-4),
m<10=(2x+4)
الحل:
m<9+m<10=180
(2x-4)+(2x+4)=180
2x-4+2x+4=180
4x=180
x=45
m<9=2x-4=2(45)-4=86
m<10=2x+4=2(45)+4=94
54) m<11=(4x),
m<12=(2x-6)
الحل:
m<11+m<12=180
(4x)+(2x-6)=180
4x+2x-6=180
6x-6=180
6x=180+6
6x=186
x=31
m<11=4x=4(31)=124
m<12= 2x-6=2(31)-6=56
55) m<19=(100+20x),
m<20=(20x)
الحل:
m<19+m20=180
(100+20x) + (20x) = 180
100+20x+20x=180
40x=180-100
40x=80
x=2
m<19=100+20x=100+20(2)=100+40=140
m<20= 20x=20(2)=40
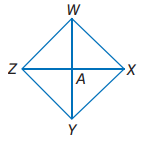
56) برهان: أكمل البرهان
الآتي:
المعطيات: WY=ZX
A
نقطة منتصف WYوZX.
المطلوب: WA=ZA
الحل:
المعطيات: WY=ZX
A
منتصف WY
A منتصف ZX
المطلوب: WA=ZA
البرهان:
1) WY=ZX،
A
منتصف WY
A منتصف ZX (معطيات)
2) WY=ZX
(تعريف تطابق القطع المستقيمة)
3) WA=AY،ZA=AX (
تعريف نقطة المنتصف)
4) WY=WA+AY,
ZX=ZA+AX ( مسلمة جمع القطع المستقيمة)
5) WA+AY=ZA+AX
( بالتعويض)
6) WA+WA=ZA+ZA
( بالتعويض)
7) 2WA=2ZA
( بالتعويض)
8) WA=ZA
( خاصية القسمة)
9) WA=ZA
( تعريف تطابق القطع المستقيمة)
57) استعمل قانون الفصل
المنطقي أو قانون القياس المنطقي، لتحصل على نتيجة صائبة إن أمكن من العبارتين
الآتيتين، و اذكر القانون الذي استعملته، وإذا تعذر الحصول على نتيجة صائبة، فاكتب
"لا نتيجة صائبة".
a)
إذا كانت الزاويتان متقابلتان بالرأس، فإنهما ليستا متجاورتين على
مستقيم.
b) إذا تجاوزت زاويتان مستقيم، فإنهما غير
متطابقتين.
الحل:
لا
نتيجة صحيحة.
جبر: في الشكل المجاور: FC ⊥AD.
58) إذا كان m<CFD=(12a+45)، فأوجد قيمة a.
الحل:
m<CFD=90
12a+45=90
12a=90-45
12a=45
a=45/12
a=3.75
59) إذا كان m<AFB=(8x-6) و m<BFC=(14x+8)، فأوجد قيمة x.
الحل:
m<AFB + m<BFC=90
(8x-6) + (14x+8) =90
22x+2=90
22x=90-2
22x=88
x=4
استعد للدرس اللاحق
أوجد قيمة x في كل مما يأتي:
60)
الحل: 90.
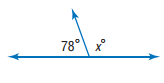
61)
الحل:
180-78 =102
62)
الحل:
3x+x=180
4x=180
x=180/4
x=45































ليست هناك تعليقات:
إرسال تعليق