حل تمارين درس 7-1 إثبات علاقات بين القطع المستقيمة - التبرير والبرهان
تأكد:
1)
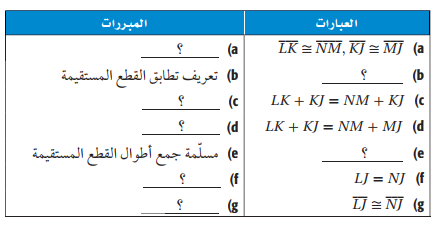
أكمل البرهان الآتي:
المعطيات:
LK=NM,KJ=MJ
المطلوب:
LJ=NJ
البرهان:
الحل:
2)
مقص: في الشكل المجاور،
AR=CR,DR=BR، أثبت أن:
AR+DR=CR+BR.
الحل:
المعطيات: AR=CR;DR=BR
المطلوب:AR+DR=CR+BR
البرهان:
تدريب وحل المسائل
3) أكمل البرهان الآتي:
المعطيات: C نقطة منتصف AE.
C نقطة منتصف BD.
AE=BD
المطلوب: AC=CD
البرهان:
الحل:
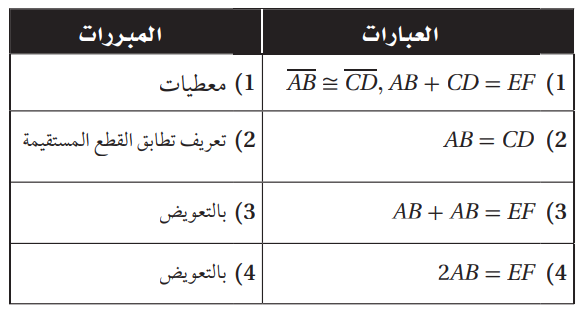
4) تبليط : قص مبلط قطعة
بلاط بطول معين، ثم استعملها نموذجا ليقص بلاطة ثانية تطابق الأولى، ثم استعمل
هاتين البلاطتين لقص بلاطة ثالثة طولها يساوي مجموع طولي البلاطتين. أثبت أن طول
البلاطة الثالثة يساوي مثلي طول البلاطة الأولى.
الحل:
المعطيات: AB+CD=EF، ِAB=CD
المطلوب: 2AB=EF
البرهان:
أثبت الخاصيتين الآتيتين في النظرية (1.2)
5) خاصية التماثل
للتطابق.
الحل:
المعطيات: AB=CD
المطلوب: CD=AB
البرهان:
6) خاصية الانعكاس
للتطابق.
الحل:
المعطيات: AB
المطلوب: AB=AB
البرهان:
برهان : أثبت كلا مما يأتي:
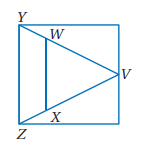
7) إذا كان VZ=VY,WY=XZ، فإن VW=VX.
الحل:
المعطيات: VZ=VY,WY=XZ
المطلوب: VW=VX
البرهان:
8) إذا كانت E نقطة منتصف DF ، CD=FG ، فإن CE=EG.
الحل:
المعطيات: E نقطة منتصف DF ، CD=FG
المطلوب: CE=EG
البرهان:
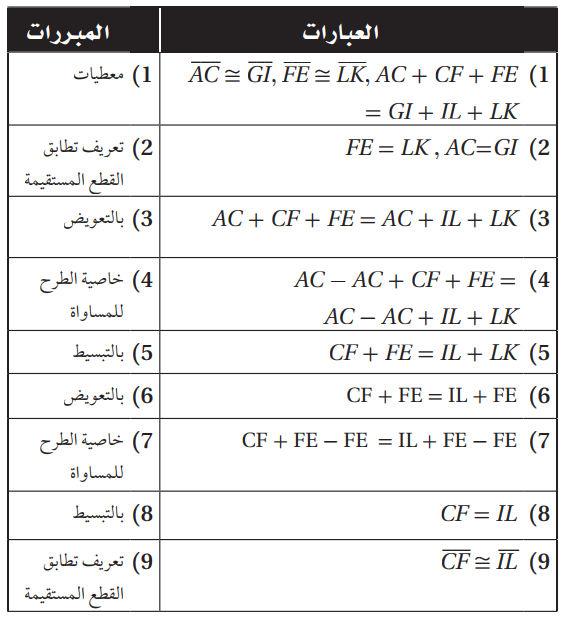
9) إذا كان AC=CI، FE=LK، AC+CF+FE=GI+IL+LK.
a) فأثبت أن CF=IL.
الحل:
المعطيات:
AC=Gl,FE=LK
,AC+CF+FE=GI+IL+LK
المطلوب: CF=IF
البرهان:
b) برر برهانك بقياس
أطوال القطع المستقيمة. فسر إجابتك.
الحل:
لقد قست CF وIL، وهما متساويتا الطول، إذن هما متطابقتان.
10)
تمثيلات متعددة: A نقطة منتصف PQ، وB نقطة منتصف PA، C نقطة منتصف PB.
a) هندسيا: ارسم شكلا
يوضح هذه المعطيات.
الحل:
b) جبريا: ضع تخمينا
للعلاقة الجبرية بين PC وPQ.
الحل:
8PC=PQ
c) حسيا: استعمل مسطرة لرسم قطعة مستقيمة تطابق PQ، و لتعيين النقطتين B و C على PQ ، استعمل هذا الرسم لتؤيد التخمين الذي وضعته.
الحل:
يمكنك قياس طول PC، ووضع علامات على PQ لقطع طول كل منها
يساوي طول PC ، ثم عد القطع
الناتجة.
d) منطقيا: أثبت صحة
تخمينك.
الحل:
المعطيات: A نقطة منتصف PQ، وB نقطة منتصف PA و C نقطة منتصف PB.
المطلوب: 8PC=PQ
البرهان:
مسائل مهارات التفكير العليا:
11)
اكتشف الخطأ: في الشكل المجاور: AB=CD,CD=BF، اختبر النتائج التي حصل عليها أحمد و سعد ،
وهل وصل أي منهما إلى نتيجة صحيحة؟
الحل:
كلاهما خطأ. الإجابة الصحيحة هي : بما أن AB=CD و CD=BF ، فإن AB=BF باستعمال خاصية التعدي للتطابق.
12)
تحد: ABCD مربع ، أثبت أن AC=BD.
الحل:
المعطيات: ABCD مربع.
المطلوب: AC=BD
13)
اكتب: هل توجد خاصية في التطابق تشبه خاصية الجمع في
المساواة؟ فسر إجابتك.
الحل:
لا، لأن التطابق صفة للقطع المستقيمة، والقطع المستقيمة لا يمكن
جمعها، في حين أن أطوال القطع المستقيمة هي أعداد يمكننا جمعها.
14)
تبرير: صنف العبارة الآتية إلى صحيحةأو خاطئة، و إذا
كانت خاطئة فأعط مثالا مضادا .
الحل:
خاطئة، مثال مضاد: في الشكل التالي: AC=BD=CE=10، ولكن AB=7، BC=3 ، CD=7 ، DE=3
15)
مسألة مفتوحة: ارسم شكلا يمثل تعميما لمسلمة جمع
أطوال القطع المستقيمة ، ( جمع 3 قطع مستقيمة) و اكتب النتيجة.
الحل:
AB+BC+CD=AD
تدريب على اختبار
16)
النقاط A,B,C,D تقع على استقامة واحدة، بحيث تقع النقطة B بين A و C والنقطة C بين B وD. أي عبارة مما يلي ليست بالضرورة صحيحة؟
A AB+BD=AD
B ِAB=CD
C BC=BC
D BC+CD =BD
الحل:
B.
17)
أي العبارات الآتية يعطي وصفا أفضل للمسلمة؟
A تخمين ينشأ عن أمثلة.
B تخمين ينشأ عن حقائق و
قواعد وتعريفات وخصائص.
C عبارة تقبل على أنها صحيحة.
D عبارة تم إثبات أنها صحتها.
الحل:
C.
مراجعة تراكمية
18)
برهان: أثبت أنه إذا كان -3(2x+1)=57، فإن x=-10، واكتب تبريرا لكل خطوة.
الحل:
البرهان:
19)
نماذج: استعمال حاتم ستة مربعات من الورق المقوى لعمل
منشور رباعي. ما الجزء من الفراغ الذي يمثله كل وجه من المنشور، وكم مستقيما ينتج
عن تقاطعها؟
الحل:
مستويات ، 12.
20)
أنماط: يمكن ترتيب مجموعة من قطع النماذج لتكوين نمط
دوراني دون ترك فراغات بين هذه القطع، وكما تعلم أن قياس الدورة الكاملة يساوي 3600
، أوجد قياس الزوايا المرقمة في كل من الأشكال الآتية بالدرجات.
الحل:
استعد للدرس اللاحق
جبر: أوجد قيمة x في كل مما يأتي:
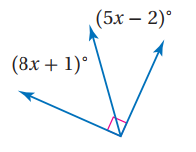
21)
الحل:
8x+1+5x-2=90
13x=90-1+2
13x=90+1
13x=91
X=91/13
X=7
22)
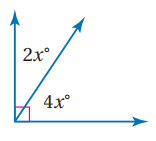
الحل:
14x+8x+4=180
22x=180-4
22x=176
X=176/22
X=8
23)
الحل:
2x+4x=90
6x=90
X=90/6
X=15
































ليست هناك تعليقات:
إرسال تعليق