حل تمارين درس 8-1 إثبات علاقات بين الزوايا - التبرير والبرهان

 

أوجد قياس الزوايا المرقمة في كل مما يأتي، واذكر النظريات التي تبرر حلك.

      1)          M<2=x,M3=(x-16)

الحل:

M<3=37⁰, m<2=53⁰، نظرية الزاويتين المتتامتين.

 

      2)  M<4=(3(x-1)),m<5=(x+7)

الحل:

M<5=51⁰, m<4=129⁰، نظرية الزاويتين المتكاملتين.

 

      3)  موقف: استعمل مخطط موقف السيارات المجاور. إذا علمت أن <2=<6 ، فأثبت أن <4=<8

الحل:

المعطيات: <2=<6

المطلوب: <4=<8

البرهان:

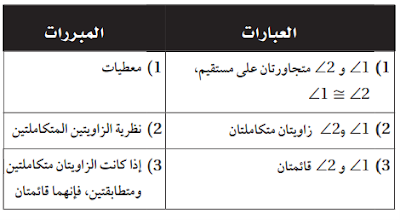
      4)  برهان: فيما يأتي أكمل برهان إحدى حالات نظرية تطابق المتممات.

المعطيات: <1 و <3 متتامتان.

              <2 و <3  متتامتان.

المطلوب: <1=<2

البرهان:

الحل:

 

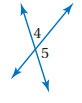
      5)  برهان: اكتب برهانا ذا عمودين فيما يأتي:

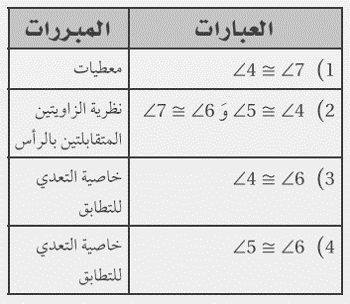
المعطيات: <4=<7

المطلوب: <5=<6

 

الحل:

المعطيات: <4=<7

المطلوب: <5=<6

البرهان:

 

تدرب وحل المسائل

أوجد قياس الزوايا المرقمة في كل مما يأتي، واذكر النظريات التي تبرر حلك.

      6)  M<5=m<6

الحل:

M<5=m<6=45، مسلمة جمع قياسات الزوايا و نظرية الزاويتين المتكاملتين.

      

      7)    <2و<3 متتامتان، <1=<4، m<2=28⁰

 

 

    الحل:

M<1=m<4=45,m<3=62 ، نظرية الزاويتين المتتامتين ومسلمة جمع قياسات الزوايا.

       8)  <2 و  <4 متكاملتان، <4 و <5 متكاملتان، m<4=105.

الحل:

M<5=75,m<3=105,m<2=75، نظرية تطابق المكملات ونظرية الزاويتين المتكاملتين.

 

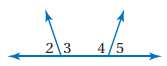
       9)  M<9=(3x+12)

    M<10=(x-24)

 

    الحل:

M<10=24,m<9=156 ، نظرية الزاويتين المتكاملتين.

 

أوجد قياس الزوايا المرقمة في كل مما يأتي، و اذكر النظريات التي تبرر حلك.

       10)                 M<3=(2x+23)

M<4=(5x-112)

الحل:

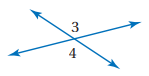
M<3=113، m<4=113 نظرية الزاويتين المتقابلتين بالرأس.

  

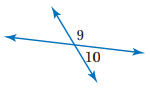
        11)                 M<6=(2x-21)

M<7=(3x-34)

الحل:

M<6=73، m<7=107، m<8=73 ، نظرية الزاويتين المتكاملتين ونظرية الزاويتين المتقابلتين بالرأس.

 

برهان: اكتب برهانا ذا عمودين في كل مما يأتي:

        12)                 المعطيات: <ABC زاوية قائمة.

المطلوب: <CBD، <ABD متتامتان.

الحل:

البرهان:

 

        13)                 المعطيات: <5=<6

المطلوب: <6,<4 متكاملتان.

الحل:

البرهان:

اكتب برهانا لكل من النظريات الآتية:

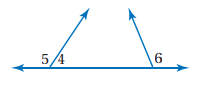
      14)                 نظرية الزاويتين المتكاملتين.

الحل:

المعطيات: <1 و<2 متجاورتان على مستقيم.

المطلوب: <1 و<2 متكاملتان.

برهان حر:

عندما تكون الزاويتين متجاورتين على مستقيم، فإن الزاوية الناتجة عنهما تكون زاوية مستقيمة قياسها 180⁰، وبالتعريف تكون الزاويتان متكاملتين، إذ كان مجموع قياسيهما 180⁰، وباستعمال مسلمة جمع الزوايا m<1+m<2=180⁰. ومن ذلك تكون الزاويتان متكاملتين، إذا كانتا متجاورتين على مستقيم.

 

     15)                 نظرية الزاويتين المتتامتين.

الحل:

المعطيات: <ABC قائمة.

المطلوب: <1 و <2 متتامتان.

البرهان:

      16)                 خاصية الانعكاس للتطابق.

الحل:

المعطيات: <A

المطلوب: <A=<A

البرهان:

 

      17)                 خاصية التعدي للتطابق.

الحل:

المعطيات: <1=<2، <2=<3

المطلوب: <1=<3

البرهان:

 

      18)                 برهان: أثبت أن مجموع قياسات الزوايا الأربع الناتجة عند فتح المقص يساوي 360⁰.

الحل:

المعطيات:

<1,<2,<3,<4 ناتجة عن تقاطع مستقيمين.

المطلوب:

M<1+m<2+m<3+m<4=360

البرهان:

      19)                 طبيعة: الأفعى المجلجلة أفعى سامة، ويوجد على جلدها زركشة تأخذ أشكالا نمطية. انظر إلى الشكل أدناه، والذي يمثل صورة مكبرة لجلد الأفعى المبينة جهة اليمين. إذا كانت <1=<4، فأثبت أن <2=<3.

 

الحل:

المعطيات: <1=<4

المطلوب: <2=<3

البرهان:

برهان: استعمل الشكل المجاور لكتابة برهان لكل من النظريات الآتية.

      20)                 نظرية 1.9

الحل:

المعطيات: l ⊥ m

المطلوب: <2,<3,<4 قوائم.

البرهان:

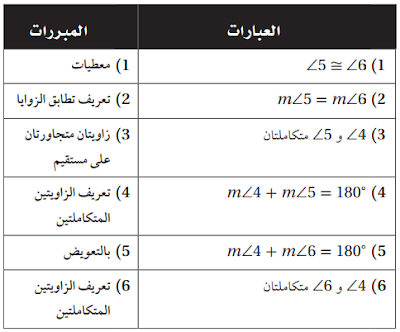
       21)                 نظرية 1.10

الحل:

المعطيات: <1 و<2 قائمتان

المطلوب:  <1=<2

البرهان:

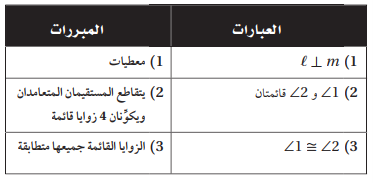
     22)                 نظرية 1.11

الحل:

المعطيات: ℓ ⊥ m

المطلوب: <1=<2

البرهان:

 

      23)                 نظرية 1.12

الحل:

المعطيات: <1 و<2 متكاملتان، <1=<2

المطلوب: <1 و<2 قائمتان.

البرهان:

    24)                 نظرية 1.13

الحل:

المعطيات: <1 و<2 متجاورتان على مستقيم، <1=<2

المطلوب:  <1 و<2 قائمتان

البرهان:

      25)                 بندول: يظهر في الشكل المجاور وضع بندول ساعة تقليدية. إذا علمت أن <ABC قائمة. وأن m<1=45، فاكتب برهانا حرا لإثبات أن  BR ينصف <ABC.

 

الحل:

بما أن <ABC قائمة، فإن قياسها يساوي 90، BR يقسم <ABC إلى <ABR و <CBR وباستعمال مسلمة جمع الزوايا m<ABR +m<CBR=m<ABC وبالتعويض m<ABR+ m<CBR=90

 وبالتعويض مرة ثانية m<1+m<2=90 وبما أن m<1=45 إذن 45+m<2=90 وباستعمال خاصية الطرح للمساواة 45-45+m<2=90-45 فإن m<2=45. وبما أن m<1 و m<2 متساو، فإن BR يكون منصفا للزاوية <ABC بتعريف منصف الزاوية.

 

      26)                 تمثيلات متعددة: في هذه المسألة سوف تستكشف علاقات الزوايا.

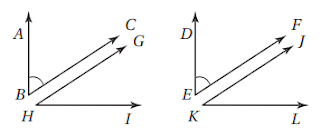
a)  هندسيا: استعمل المنقلة لرسم زاوية قائمة ABC، وحدد نقطة داخلها، وسمها D.ارسم BD. ثم ارسم KL، وارسم <JKL التي تطابق <ABD.

الحل:

b)  لفظيا: ضع تخمينا حول العلاقة بين <JKL و<DBC.

الحل:

<DBC و JKL متتامتان.

 

c)   منطقيا: أثبت صحة التخمين الذي وضعته.

الحل:

              المعطيات: <ABD و <DBC متتامتان.

                        <ABD=<JKL

                 المطلوب: <DBC و <JKL متتامتان.

               البرهان:

 

 

مسائل مهارات التفكير العليا:

      27)                 تحد: لقد تم إثبات حالة واحدة من نظرية تطابق المكملات، وفي السؤال 4  برهنت الحالة المشابهة من نظرية تطابق المتممات. فسر لماذا توجد حالتان لكل من هاتين النظريتين، اكتب برهانا للحالة الثانية لكل منهما.

الحل:

المعطيات: <ABC=<DFE ، <GHI متممة <ABC،  <JKL متممة  <DEF.

المطلوب: <GHI=<JKL

البرهان:

المعطيات: <ABC=<DEF، <GHI مكملة <ABC، <JKL مكملة <DEF.

المطلوب: <GHI=<JKL

البرهان:

 

      28)                 تبرير: حدد ما إذا كانت العبارة الآتية صحيحة أحيانا أو صحيحة دائما أو غير صحيحة أبدا. فسر تبريرك.

"إذا كانت إحدى الزوايا المتكونة من مستقيمين متقاطعين حادة، فإن الزوايا الثلاث الأخرى المتكونة من هذا التقاطع حادة أيضا"

الحل:

غير صحيحة أبدا ، لأن كل زاويتين متجاورتين ناشئتان من تقاطع مستقيمين، تكونان متجاورتين على مستقيم. وإذا كانت إحدى هاتين الزاويتين حادة فسيكون قياسها أقل من 90، وسيكون قياس مكملتها أكثر من 90، لأن ناتج طرح عدد أقل من 90 من العدد 180 سيكون عددا أكبر من 90 دائما.

 

      29)                 اكتب: فسر كيف يمكن استعمال المنقلة لإيجاد قياس الزوايا المتممة لزاوية أخرى بطريقة سريعة.

الحل:

بما أن المنقلة تتضمن تدريجا للزوايا الحادة وآخر للزوايا المنفرجة، فإن قياس المكملة هو القياس المقابل لقياس الزاوية المعلومة على التدريج الآخر من المنقلة.

تدرب على اختبار

      30)                 في الشكل المجاور إذا كانت النقاط E، F ، B تقع على استقامة واحدة، وكذلك النقاط A,F,D، فأوجد قياس <CFD

a)  66

b)  72

c)   108

d) 138 

    الحل:

           A.      

      31)                 إذا كانت النسبة بين قياسي زاويتين متتامتين هي 4:1 فما قياس الزاوية الصغرى؟

a)  15

b)  18

c)   24

d)  36

   الحل: B.

 

مراجعة تراكمية

       32)                 خرائط: يظهر الشكل المجاور مقياس رسم خريطة تدريجين أحدهما بالكيلومترات، والآخر بالأميال. إذا كانت AB و CD قطعتين مستقيمتين على الخريطة، حيث AB=100km ، CD=62 mi. فهل AB=CD؟ فسر إجابتك.

الحل:

نعم ، بحسب مقياس الرسم المعطى 100km=62mi، إذن AB=CD، وبتعريف تطابق القطع المستقيمة فإن AB=CD.

 

اذكر الخاصية التي تبرر كل عبارة مما يأتي:

      33)                 إذا كان y+7=5 ، فإن y=-2.

الحل:

خاصية الطرح للمساواة.

      34)                 إذا كان MN=PQ، فإن PQ=MN

الحل:

خاصية التماثل للمساواة

      35)                 إذا كان a-b=x و b=3 ، فإن a-3=x

الحل:

خاصية التعويض للمساواة.

      36)                 إذا كان x(y+z)=4 ،  فإن xy+xz=4.

الحل:

خاصية التوزيع.

 

استعد للدرس اللاحق

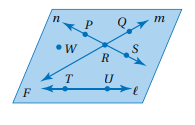
استعمل الشكل المجاور للإجابة عما يأتي:

 

       37)                 سم مستقيما يحوي النقطة P.

الحل: المستقيم n.

      38)                 سم تقاطع المستقيمين n وm.

الحل: النقطة R.

      39)                 سم نقطة لا تقع على أي من المستقيمات l,m,n.

الحل: النقطة W.

      40)                 اذكر اسما آخر للمستقيم n.

        الحل: PR

      41)                 هل يتقاطع المستقيم l مع المستقيم m أو المستقيم n؟ فسر إجابتك.

الحل:

نعم، يتقاطع المستقيم l مع كل من المستقيمين m و n، وذلك عند مد المستقيمات الثلاثة.