حل تمارين درس 2-2 الزوايا والمستقيمات المتوازية - التوازي والتعامد
تأكد:
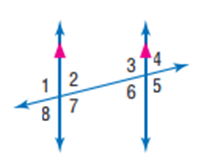
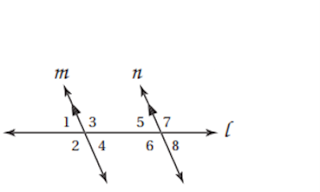
في الشكل المجاور: m<1=94o. أوجد قياس كل من الزوايا الآتية، واذكر المسلمات أو النظريات التي استعملتها:
1) <3
الحل:
1> = 3> = 94، مسلمة الزاويتين المتناظرتين.
2) <5
الحل:
1> = 5> = 94،
نظرية الزاويتين المتبادلتين خارجيا.
3) <4
الحل:
5> و 4> زاويتين متجاورتين على استقامة واحدة.
4> = 180-94 = 86، مسلمة الزاويتين المتناظرتين ونظرية الزاويتين المتكاملتين.
في الشكل المجاور: m<4=101o.
أوجد قياس كل من الزوايا الآتية، واذكر المسلمات أو النظريات التي استعملتها:
4) <6
الحل:
4> = 6> = 101، نظرية الزاويتين المتبادلتين داخليا.
5) <7
الحل:
4> , 5> متحالفتان إذا مجموعهم يساوي 180.
وعليه فإن 5> = 101-180 = 79
, 5> تساوي 7> بالتقابل بالرأس.
7> = 79، نظرية الزاويتين المتقابلتين بالرأس، ونظرية الزاويتين المتحالفتين.
6) <5
الحل:
4> و 5> متحالفتان إذا مجموعهما يساوي 180.
وعليه فإن 5> =101-180 = 79
5> = 79، نظرية الزاويتين المتحالفتين.
7) طرق: حاجز الحماية في الشكل المجاور يوازي سطح الطريق، والدعامات
الرأسية يوازي بعضها بعضا. أوجد قياس الزوايا 2,3,4.
الحل:
m<2=93o, m<3=87o, m<4=87o.
أوجد قيمة كل متغير في الأشكال الآتية. برر إجابتك:
8)
الحل:
x=125
نظرية الزاويتين المتكاملتين، y=125 نظرية
الزاويتين المتبادلتين داخليا.
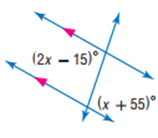
9)
الحل:
x=114
نظرية الزاويتين المتبادلتين خارجيا.
10)
الحل:
x=70
نظرية الزاويتين المتبادلتين داخليا.
11) إجابة قصيرة: إذا كان m||n، فأوجد قيمة x. بين خطوات حلك.
الحل:
4x-23=2x+17
4x-2x=23 + 17
2x= 40
x=20
في
الشكل المجاور: m<11=22o،
و m<14=18o،
أوجد قياس كل من الزوايا الآتية، واذكر المسلمات أو النظريات التي استعملتها:
12)
<4
الحل:
4> =11> = 22، مسلمة الزاويتين المتناظرتين.
13)
<3
الحل:
3> = 4> = 22، بالتقابل بالرأس.
14)
<2
الحل:
1> = 14> , 3> = 11> بالتبادل خارجيا.
1> + 2> +3> = 180 زوايا متجاورة على استقامة واحدة.
180 = 18+ 2> + 22
40 - 180 = 2>
2> = 140
140،
نظرية الزاويتين المتبادلتين خارجيا و نظرية الزاويتين المتكاملتين.
15)
<10
الحل:
10> +14> = 180
10> + 18 = 180
10> = 162
162،
نظرية الزاويتين المتكاملتين.
16)
<5
الحل:
5> = 2> = 140، نظرية الزاويتين المتقابلتين بالرأس.
17)
<1
الحل:
1> = 14> = 18، نظرية الزاويتين المتبادلتين خارجيا.
طاقة شمسية: يجمع الطبق الشمسي الطاقة بتوجيه أشعة الشمس نحو مستقبل يقع في بؤرة الطبق. مفترضا أن أشعة الشمس متوازية، حدد العلاقة بين أزواج الزوايا الآتية. برر إجابتك:
18)
<1
و<2
الحل:
متكاملتان،
لأنهما زاويتان متحالفتان.
19)
<1
و<3
الحل:
متطابقتان،
لأنهما زاويتان متناظرتان.
20)
<4
و <5
الحل:
متطابقتان،
لأنهما زاويتان متبادلتان خارجيا.
21)
<3
و<4
الحل:
متكاملتان،
بما أن <3
و <5
متجاورتان على مستقيم فإنهما متكاملتان. <4 و <5
متطابقتان لأنهما زاويتان متبادلتان خارجيا لذا فإن <3 تكمل
<4.
أوجد قيمة كل متغير في الاشكال الآتية. برر إجابتك:
22)
الحل:
حسب مسلمة الزاويتين المتناظرتين:
حسب نظرية الزاويتين المتكاملتين:
x=40,y=50
23)
الحل:
x=63
24)
الحل:
x=54, y=12
إذا كان m||n، فأوجد قيمة x في
كل مما يأتي، حدد المسلمة أو النظرية التي استعملتها:
25)
الحل:
39،
نظرية الزاويتين المتبادلتان خارجيا.
26)
الحل:
22،
مسلمة الزاويتين المتناظرتين.
27)
الحل:
27 ،
نظرية الزاويتين المتبادلتين داخليا.
28)
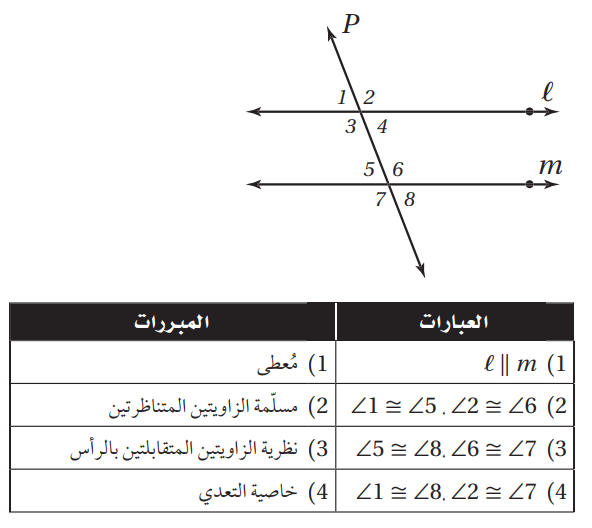
برهان: أكمل النظرية 2.2.
المعطيات: m||n،
l قاطع للمستقيمين n، m.
المطلوب: <1,<2 متكاملتان، <3,<4 متكاملتان.
البرهان:
الحل:
تخزين: عند تركيب الرفوف، تضاف دعامات جانبية متقاطعة. حدد العلاقة بين كل زوج من الزوايا فيما يأتي. برر إجابتك:
29)
<1
و<8
الحل:
متطابقتان،
زاويتان متبادلتان داخليا.
30)
<1
و <5
الحل:
متطابقتان،
زاويتان متناظرتان.
31)
<3
و<6
الحل:
متطابقتان،
زاويتان متقابلتان بالرأس.
32)
<1
و<2
الحل:
متتامتان،
لأن المستقيمين الرأسي والأفقي متعامدان ويشكلان زوايا قائمة.
33)
برهان: اكتب برهانا ذا عمودين لنظرية الزاويتين المتبادلتين خارجيا.
الحل:
المعطيات:
L||m،
P
قاطع
المطلوب:
<1=<8
<2=<7
البرهان:
34)
برهان: أثبت أنه إذا كان مستقيم عموديا على أحد مستقيمين متوازيين في
مستوى، فإنه يكون عموديا على الآخر.
الحل:
المعطيات:
m||n،
t ⊥ m
المطلوب:
t ⊥ m
أوجد قيمة x في
كل من الشكلين الآتيين:( إرشاد: ارسم مستقيما مساعدا)
35)
الحل:
x=22
36)
الحل:
x=130
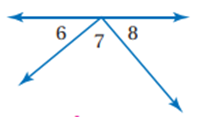
37) احتمالات: افترض أنك اخترت عشوائيا زوجا من الزوايا في الشكل المجاور.
a) ما عدد الطرق الممكنة لاختيار زوج
الزوايا؟ برر إجابتك.
b) صف العلاقات الممكنة بين زاويتي كل
زوج. برر إجابتك.
c) أوجد احتمال اختيار زوج من الزوايا
المتطابقة. برر إجابتك.
الحل:
a) يوجد 28 زوجا من الزوايا، حيث يمكن تشكيل سبعة
أزواج من الزوايا من الزاوية الأولى، وستة أزواج من الزوايا مع الزاوية الثانية،
لأنها شكلت زوجا مع الزاوية الأولى، وهكذا فإن عدد أزواج الزوايا يساوي:
1+2+3+4+5+6+7 أو 28 زوجا.
b) توجد علاقتان ممكنتان بين أزواج الزوايا، فإذا
اخترنا زاويتين، فإنهما إما متطابقتان أو متكاملتان.
c) اثنى عشر زوجا من الزوايا المتطابقة ،و 16 زوجا
منها متكاملة ، لذا فاحتمال أن تكون الزاويتان في زوج الزوايا متطابقتين هو 12/28
أي 3/7.
بينما احتمال كونهما متكاملتين هو 16/28 أي 4/7.
38)
تمثيلات متعددة: ستبحث في هذه المسألة العلاقة بين الزوايا الخارجية
الواقعة في الجهة نفسها.
a) هندسيا: ارسم خمسة أزواج من المستقيمات
المتوازية m وn،
a وb ، r
وs ، j وk
، x وy يقطع كلا منها قاطع t، ثم قس جميع الزوايا الناتجة. ( يمكنك استخدام الآلة البيانية في
هذا التمرين)
b) جدوليا: دون بياناتك في جدول.
c) لفظيا : ضع تخمينا حول العلاقة بين
الزاويتين الخارجيتين الواقعتين في جهة واحدة من القاطع
d) منطقيا: ما نوع التبرير الذي استعملته
لوضع تخمينك؟ برر إجابتك.
e) برهان: برهن تخمينك.
الحل:
a)
b)
c) الزاويتان الخارجيتان الواقعتان في جهة واحدة مع القاطع متكاملتان.
d) التبرير الاستقرائي، ثم استعمال نمط للوصول إلى
النتيجة.
e) المعطيات: المستقيمان m و n
متوازيان ويقطعهما المستقيم t.
المطلوب:
<1 و <4 متكاملتان.
مسائل مهارات التفكير العليا:
39) اكتب: إذا كان المستقيم a يوازي المستقيم b، و<1=<2. فصف العلاقة بين المستقيمين b وc. وبرر إجابتك.
الحل:
المستقيمان
b
وc
متعامدان، بما أن <1 و<2
متجاورتان على مستقيم، فإن m<1+m<2=180، لكن <1
تطابق <2،
لذا m<1=m<2،
بالتعويض m<1+m<1=180،
لذا m<1=90
و m<2=90،
لذا فالمستقيمان a
وc
متعامدان، بحسب النظرية 2.4، وبما أن c
عمودي على المستقيم a والمستقيم a وb
متوازيان، فإن المستقيم c
عمودي على المستقيم b أيضا.
40)
اكتب: حدد أوجه الشبه والاختلاف بين نظرية الزاويتين المتبادلتين
داخليا، ونظرية الزاويتين المتحالفتين.
الحل:
في
كلتا النظريتين يتكون زوج من الزوايا، عندما يقطع قاطع مستقيمين متوازيين. ومع ذلك
ففي نظرية الزاويتين المتبادلتين داخليا، يكون مل زوج من الزوايا المتبادلة داخليا
متطابقا. في حين يكون كل زوج من الزوايا المتحالفة متكاملا في نظرية الزاويتين
المتحالفتين.
41) تحد: أوجد جميع قيم x,y في الشكل المجاور.
الحل:
y2=8y-15
y2-8y+15=0
(y- 5)(y-3 )=0
y=5 أو y=3
x+8y-15=180
بالتعويض
عن قيمة y=5
في المعادلة السابقة فإن
x+8(5)-15=180
x=180-40+15
x=155
وبالتعويض
عن قيمة y=3
في المعادلة x+8y-15=180
فإن
x+8(3)-15=180
x+24-15=180
x=180-24+15
x=171
42)
تبرير: ما أقل عدد من قياسات الزوايا التي يجب معرفتها حتى يكون
بمقدورك تحديد قياسات جميع الزوايا الناتجة عن مستقيمين متوازيين يقطعهما قاطع؟
وضح إجابتك.
الحل:
يكفي معرفة قياس زاوية واحدة، لأن الزوايا
الباقية إما مطابقة لها أو مكملة.
تدريب على اختبار
43)
افترض أن <5، <4
متجاورتان على مستقيم، إذا كان m<3=(x-4)0,
m<2=(3x-20)0, m<1=(2x)0، فما قيمة m<3؟
a) 260
b) 280
c) 300
d) 320
الحل:
C.
طريقة
الحل:
m<1+m<2+m<3=180
(2x)+(3x-20)+(x-4)
2x+3x-20+x-4
6x-24=180
6x=180+24
6x=204
x=34
ومنه فإن
m<3 = x-4 = 34-4 =30
44)
إجابة قصيرة: إذا كان m||n، حدد أي العبارات الآتية
صحيحة، وأيها خاطئة. وبرر إجابتك؟
1. <3,<6 متبادلتان داخليا.
2. <4,<6 متحالفتان.
3. <1,<7 متبادلتان خارجيا.
الحل:
1. صحيحة، لأن <3,<6
داخليتان وغير متجاورتين وتقعان في جهتين مختلفتين من القاطع L.
2. صحيحة، لأن <4,<6
داخليتان وواقعتان في جهة واحدة من القاطع L.
3. خاطئة، لأن <1,<7
تقعان على الجهة نفسها من القاطع L.
مراجعة تراكمية:
حدد كلا مما يأتي مستعملا الشكل المجاور:
45)
جميع القطع المستقيمة التي توازي AB.
الحل: FG.
46)
جميع القطع المستقيمة التي تخالف CH.
الحل: AB,DE,FG,IJ,AE,FJ
47)
جميع المستويات التي توازي AEF.
الحل: DCH.
48)
إذا كانت <1,<2 متجاورتين على مستقيم، وm<2=670، فأوجد m<1.
الحل:
m<1+m<2=180
m<1+67=180
m<1=180-67
m<1=113
49) إذا كانت <6,<8 متتامتين، وm<8=47، فأوجد m<6,m<7.
الحل:
m<6+m<8=90 و m<6+m<7+<8=180
m<6+47=90
m<6=90-47
m<6= 43
m<6+m<7+m<8=180
43+m<7+47=180
m<7=180-47-43
m<7=180-90
m<7=90
50) إذا كان m<4=320، فأوجد m<5,m<3.
الحل:
m<3=90
m<5+m<4=90
m<5+32=90
m<5=90-32
m<5=58
51)
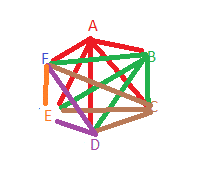
قطارات: وضع مهندس مخططا لشبكة سكك حديدية تصل بين المدن A,B,C,D,E,F، فرسم قطعة مستقيمة بين كل مدينتين على الخريطة، ولاحظ أن أي ثلاث
مدن منها لا تقع على استقامة واحدة. ما عدد القطع المستقيمة التي رسمها المهندس؟
الحل:
15.
للتوضيح:
استعد للدرس اللاحق:
حدد العلاقة بين كل زوج من الزوايا فيما يأتي:
52)
<1,<12
الحل: متبادلتان خارجيا.
53)
<7,<10
الحل: متحالفتان.
54)
<4,<8
الحل: متناظرتان.
55)
<2,<11
الحل: متبادلتان خارجيا.





















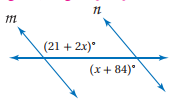




























ليست هناك تعليقات:
إرسال تعليق