حل تمارين درس 3-2 إثبات توازي مستقيمين - التوازي والتعامد
تأكد:
هل يمكن إثبات أن أيا من مستقيمات الشكل متوازية، اعتمادا على المعطيات في كل مما يأتي؟ وإذا كان أيها متوازيا، فاذكر المسلمة أو النظرية التي تبرر إجابتك.
1) <1=<3
الحل:
J||K، عكس
مسلمة الزاويتين المتناظرتين.
2) <2=<5
الحل:
J||K، عكس
نظرية الزاويتين المتبادلتين داخليا.
3) <3=<10
الحل:
L||m، عكس
نظرية الزاويتين المتبادلتين خارجيا.
4) m<6+m<8=180
الحل:
L||m،عكس
نظرية الزاويتين المتحالفتين.
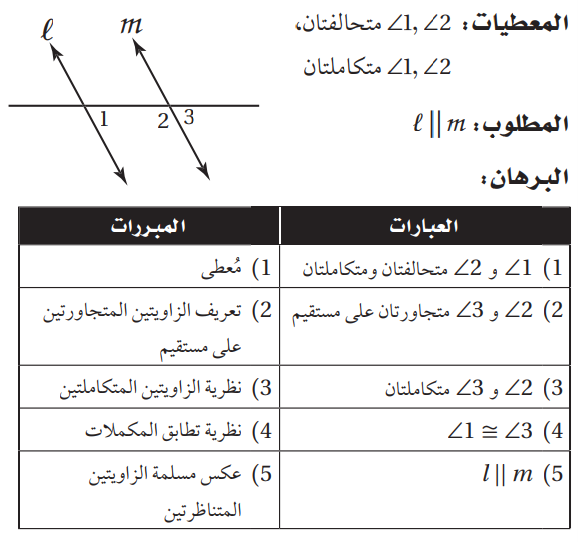
5) برهان: أكمل برهان النظرية 2.5.
المعطيات:
<1=<2
المطلوب:
L||m
البرهان:
الحل:
6)
كراسي: هل يمكن إثبات أن مسند الظهر و مسند القدمين لكرسي الاسترخاء في
الشكل المجاور متوازيان؟ وضح ذلك إذا كان صحيحا، وإلا فاذكر السبب.
الحل:
نعم، بما أن الزاويتين المتبادلتين داخليا متطابقتان، إذن مسندي الظهر والقدمين متوازيان.
تدرب وحل المسائل:
هل يمكن إثبات أن أيا من مستقيمات الشكل متوازية، اعتمادا على المعطيات في كل مما يأتي؟ وإذا كان أيها متوازيا، فاذكر المسلمة أو النظرية التي تبرر إجابتك.
7) <1=<2
الحل:
r||s، عكس
مسلمة الزاويتين المتناظرتين.
8) <2=<9
الحل:
u||v، عكس
نظرية الزاويتين المتبادلتين خارجيا.
9) m<7+m<8=180
الحل:
r||s، عكس
نظرية الزاويتين المتحالفتين.
10)
m<3+m<6=180
الحل:
u||v،عكس
نظرية الزاويتين المتحالفتين.
11)
<3=<7
الحل:
لا
يمكن إثبات التوازي اعتمادا على هذا المعطى.
12)
<4=<5
الحل:
r||s، عكس مسلمة الزاويتين المتناظرتين.
13) حدائق: لبناء سياج حول حديقة المنزل، ثبت سعود دعامات السياج، ووضع ألواحا خشبية تميل بزاوية مع كل من دعامتي السياج. وعند تثبيته أوتاد السياج، حرص على أن تكون الزوايا بين الألواح الخشبية والأوتاد متساوية القياس. لماذا يجعل هذا الأوتاد متوازية؟
الحل:
عندما يقيس
سعود الزاوية الحادة التي يصنعها كل وتد في السياج مع لوح الخشب، فإنه يقيس زاويا
متناظرة، متطابقة، فإن الأوتاد يجب ان تكون متوازية.
14)
برهان: اكتب برهانا ذا عمودين للنظرية 2.6.
الحل:
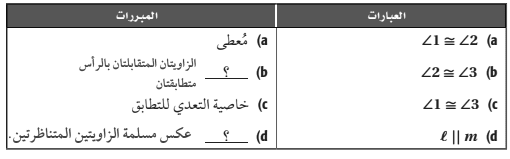
برهان: اكتب برهانا ذا عمودين لكل مما يأتي:
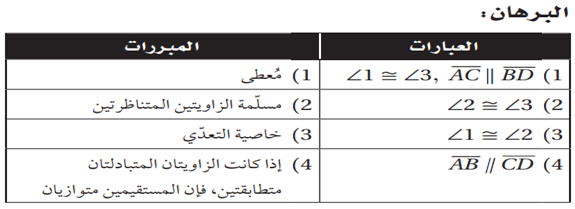
15)
المعطيات: <1=<3
AC||BD
المطلوب: AB||CD
الحل:
16)
المعطيات: <1=<2
ML ⊥ LJ
المطلوب: ML⊥ KM
الحل:
برهان: اكتب برهانا حرا لكل من النظريتين الآتيتين:
17)
النظرية 2.7
الحل:
18) النظرية 2.8
الحل:
19)
درج: ما العلاقة بين حواف أسطح الدرجات في الشكل المجاور؟ برر إجابتك.
الحل:
حواف
أسطح الدرجات متوازية، لأن الزاويتين المتناظرتين متطابقتان.
حدد ما إذا كان المستقيمان r,s
متوازيين أم لا في كل مما يأتي. برر إجابتك.
20)
الحل:
r||s 32+32=64، إذن الزاويتان المتناظرتان متطابقتان، لذا
فإن المستقيمين متوازيان.
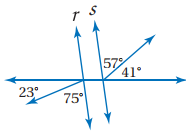
21)
الحل:
r||s بما
أن 41+57=23+75=98،
إذن الزاويتان المتبادلتان خارجيا متطابقتان، لذا فإن المستقيمين متوازيان.
22)
الحل:
r||s بما
أن 27+65=92،
إذن الزاويتان المتبادلتان خارجيا متطابقتان، لذا فإن المستقيمين متوازيان.
23)
تمثيلات متعددة: سوف تستكشف في هذه المسألة أقصر مسافة بين مستقيمين
متوازيين.
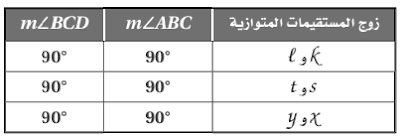
a) هندسيا: ارسم ثلاثة أزواج من المستقيمات المتوازية x وs,y وk,t وL، وارسم أقصر قطعة مستقيمة BC بين كل مستقيمين متوازيين، وعين النقطتين A,D كما في الشكل أدناه.
الحل:
b) جدوليا: قس <ABC و<BCD في كل زوج، ثم أكمل الجدول.
الحل:
c) لفظيا: ضع تخمينا حول الزاوية بين أقصر
قطعة مستقيمة وكل من المستقيمين المتوازيين.
الحل:
قياس
الزاوية التي تكونها القطعة المستقيمة مع المستقيمين المتوازيين 900.
مسائل مهارات التفكير العليا:
24)
اكتشف الخطأ: يحاول كل من سامي ومنصور تحديد المستقيمات المتوازية في
الشكل المجاور. فقال سامي : بما أن <1=<2، إذن WY||XZ. أما منصور فلم يوافقه وقال: بما أن <1=<2، إذن WX||YZ. أي منهما على صواب؟ وضح
إجابتك.
الحل:
إجابة منصورصحيحة ،
بما أن <1،<2
متبادلتان داخليا فإن YZ||WX.
25)
تبرير: هل تبقى النظرية 2.8 صحيحة إذا كان المستقيمان
لا يقعان في المستوى نفسه؟ ارسم شكلا يبرر إجابتك.
الحل:
26)
مسألة مفتوحة: ارسم المثلث ABC.
a) أنشئ مستقيما يوازي BC ويمر بالنقطة A.
b) استعمل القياس، لتتحقق من أن المستقيم
الذي رسمته يوازي BC.
c) أثبت صحة الإنشاء رياضيا.
الحل:
a)
b) باستعمال المسطرة، نجد أن البعد بين المستقيمين
ثابت، لذا فهما متوازيان.
c)
AB قاطع
لكل من BC
وAD
ونسخت <ABC
لإنشاء <EAD
، لذا فإن <ABC=<EAD
، <ABC
و<EAD
متناظرتان، بحسب عكس مسلمة الزاويتين المتناظرتين فإن AD||BC.
27)
تحد: استعمل الشكل المجاور.
a) إذا كان: m<1+m<2=180، فبرهن أن a||c.
b) إذا كان: a||c وm<1+m<3=180، فبرهن أن t⊥c.
الحل:
a) نعلم أن m<1+m<2=180.
بما أن <2
و<3
متجاورتان على مستقيم، فإن m<2+m<3=180. وبالتعويض m<1+m<2=m<2+m<3.
وبطرح m<2
من كلا الطرفين نحصل على m<1=m<3. أي أن <1=<3 بحسب
تعريف الزوايا المتطابقة، لذا فإن a||c، لأن الزاويتين المتناظرتين متطابقتين.
b) نعم أن: a||cو m<1+m<3=180. بما أن <1 و <3 متناظرتان، فإنهما متطابقتان وقياساهما متساويان. وبالتعويض: m<3+m<3=180 أو 2m<3 =180. وبقسمة كلا الطرفين على 2، نحصل على m<3=90، لذلك t ⊥ c، لأنهما يشكلان زاوية قائمة.
28)
اكتب: لخص الطرائق الخمس التي استعملت في هذا الدرس لإثبات توازي
مستقيمين.
الحل:
استعمل زاويتين متبادلتين خارجيا ناتجتين عن مستقيمين وقاطع، وبين أنهما متطابقتان، أو بين أن زاويتين متحالفتين متكاملتان، أو بين أن زاويتين متبادلتين داخليا متطابقتان، أو بين أن مستقيما يقع في نفس المستوى عمودي على كلا المستقيمين، أو بين أن زاويتين متناظرتين متطابقتان.
تدريب على اختبار:
29)
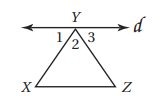
أي الحقائق الآتية كافية لإثبات أن المستقيم d
يوازي XZ؟
a) <1=<3
b) <3=<Z
c) <1=<Z
d) <2=<X
الحل:
B.
30)
استعمل الشكل المجاور لتحديد أن صحة أي مما يأتي ليست مؤكدة:
a) <4=<7
b) <4 و <8
متكاملتان
c) L||m
d) <5 و <6 متكاملتان
الحل:
C.
مراجعة تراكمية:
أعط مثالا مضادا لتبين خطأ كل تخمين في السؤالين الآتيين:
31)
المعطيات: <1,<2 متتامتان.
التخمين: <1,<2 تكونان زاوية قائمة.
الحل:
32)
المعطيات: W,X,Y,Z أربع نقاط.
التخمين: النقاط W,X,Y,Z لا تقع على استقامة واحدة.
الحل:
احسب قيمة x,y على الشكل التالي:
الحل:
مكملة ال60 تساوي 120 و120 هنا هي زاوية متبادلة
داخليا مع y
وعليه فإن قيمة Y
تساوي 120 ومكملة ال120 هي 60 وعليه فإن:
2x+10=60
2x=60-10
2x=50
x=25
استعد للدرس اللاحق
بسط كلا من العبارات الآتية:
33)
6-5/4-2
الحل:
6-5/4-2
1/2
34)
-11-4/12-(-9)
الحل:
-11-4/12-(-9)
-15/21
بقسمة
كل من البسط والمقام على 3
-5/7
35)
16-12/15-11
الحل:
16-12/15-11
4/4
1


































ليست هناك تعليقات:
إرسال تعليق