حل تمارين درس 4-2 ميل المستقيم – التوازي والتعامد
أوجد ميل كل مستقيم فيما يأتي:
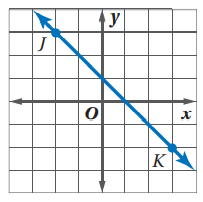
1)
الحل:
بالنظر إلى الرسم نستطيع إيجاد
النقطة j
والنقطة K
من خلال النظر إلى موقع كل منهما على الرسم وعليه فإن:
J= (-2,3), K (3, -2)
صيغة الميل:
بالتعويض في القانون السابق:
2)
الحل:
بالنظر إلى الرسم نستطيع إيجاد
النقطة T
والنقطة Uمن خلال النظر
إلى موقع كل منهما على الرسم وعليه فإن:
T= (-2,2), U (-2, -2)
صيغة الميل:
بالتعويض في القانون السابق:
وبما أن العدد 4 مقسوم على صفر فإن
قسمة أي عدد على صفر تجعل الميل غير معرف.
3)
الحل:
بالنظر إلى الرسم نستطيع إيجاد
النقطة A
والنقطة B
من خلال النظر إلى موقع كل منهما على الرسم وعليه فإن:
A= (1,1.5), B (-1.5, -1.5)
صيغة الميل:
بالتعويض في القانون السابق:
ملاحظة: إلى
هنا يكون الحل انتهى ولكن لمن يرغب في التخلص من النصف الموجود في المقام فإننا
نقوم بضرب كل من البسط والمقام في 2 وعليه تكون قيمة الميل:
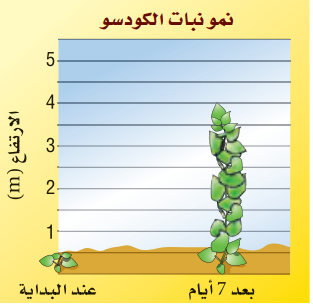
4) علم النبات: الكودسو (Kudzu) هو نبات متسلق سريع النمو. قيس ارتفاع نبتة عند يوم البداية فكان 0.5 m، وبعد سبعة أيام أصبح ارتفاعها 4m.
a) مثل بيانا المستقيم الذي يمثل ارتفاع
النبتة مع مرور الزمن.
b) ما ميل هذا المستقيم؟ وماذا يمثل؟
c) افترض أن هذه النبة استمرت في النمو وفق هذا المعدل، فكم يكون ارتفاعها بعد 15 يوما؟
الحل:
a.
b. لإيجاد الميل فإننا نقوم
باختيار أي نقطتين على الرسم السابق.
النقطة الأولى (11,6)
النقطة الثانية (7,4)
صيغة الميل:
بالتعويض في القانون السابق:
إذا فإن ميل المستقيم هو 0.5، وهو يمثل معدل زيادة طول النبتة يوميا.
c. لحساب طول النبتة نقوم بالتالي:
طول النبتة = عدد الأيام X 0.5
=
15 X
0.5
=
7.5m
وبما أن طول النبتة في اليوم الأول
هو 0.5
فإن طول النبتة الكلي هو 8m.
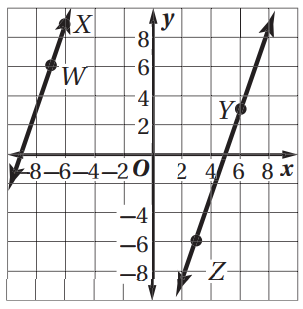
حدد ما إذا كان YZ، WX متوازيين أو متعادلين أو غير ذلك في كل مما
يأتي، ومثل كل مستقيم بيانيا لتتحقق من إجابتك.
5) W(2,4),X(4,5),Y(4,1),Z(8,-7)
الحل:
6) W(1,3),X(-2,-5),Y(-6,-2),Z(8,3)
الحل:
7) W(-7,6),X(-6,9),Y(6,3),Z(3,-6)
الحل:
8) W(1,-3),X(0,2),Y(-2,0),Z(8,2)
الحل:
مثل بيانيا المستقيم الذي يحقق الشروط في كل مما يأتي:
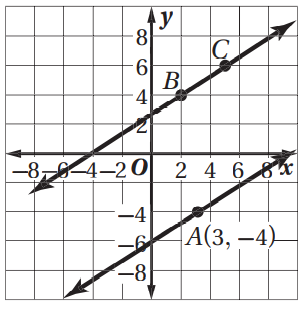
9) يمر بالنقطة A(3,-4)، ويوازي BC، حيث B(2,4), C(5,6).
الحل:
10)
ميله يساوي 3، ويمر بالنقطة A(-1,4).
الحل:
11)
يمر بالنقطة P(7,3)، ويعامد LM، حيث L(-2,-3),M(-1,5).
الحل:
تدرب وحل المسائل:
أوجد ميل كل مستقيم فيما يأتي:
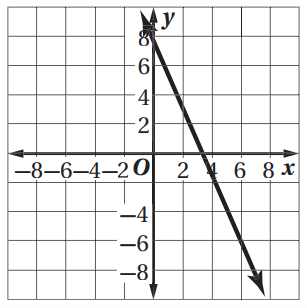
12)
الحل:
لإيجاد الميل فإننا نقوم باختيار أي
نقطتين على الرسم السابق.
النقطة D (5,5)
النقطة C (-2,-1)
صيغة الميل:
بالتعويض في القانون السابق:
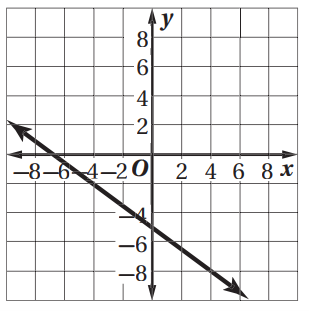
13)
الحل:
لإيجاد الميل فإننا نقوم باختيار أي
نقطتين على الرسم السابق.
النقطة M (-4,1)
النقطة N (1,-3)
صيغة الميل:
بالتعويض في القانون السابق:
14)
الحل:
لإيجاد الميل فإننا نقوم باختيار أي
نقطتين على الرسم السابق.
النقطة R (5,3)
النقطة S (5,-2)
صيغة الميل:
بالتعويض في القانون السابق:
الميل غير معرف.
أوجد ميل المستقيم الذي يمر بالنقطتين المحددتين في كل مما يأتي:
15)
C(3,1), D(-2,1)
الحل:
صيغة الميل:
بالتعويض في القانون السابق:
16)
E(5,-1), F(2,-4)
الحل:
صيغة الميل:
بالتعويض في القانون السابق:
17)
G(-4,3),H(-4,7)
الحل:
صيغة الميل:
بالتعويض في القانون السابق:
18)
J(7,-3),K(-8,-3)
الحل:
صيغة الميل:
بالتعويض في القانون السابق:
19)
P(-3,-5),Q(-3,-1)
الحل:
صيغة الميل:
بالتعويض في القانون السابق:
20)
R(2,-6),S(-6,5)
الحل:
صيغة الميل:
بالتعويض في القانون السابق:
21)
حواسيب: في عام 1423 هـ كان ثمن حاسوب محمول 3000 ريال، و أصبح 1800
ريال في عام 1427 هـ.
a) ارسم مستقيما يمثل توقعا لسعر الحاسوب
للسنوات من 1423هـ إلى 1427 هـ.
b) كم ينخفض ثمن الحاسوب في كل سنة؟
c) إذا استمر انخفاض السعر بالمعدل نفسه،
فكم يكون ثمن الحاسوب عام 1430 هـ؟
الحل:
a.
b. لإيجاد معدل انخفاض ثمن الحاسوب في كل سنة فإننا
نقوم بطرح ثمن الحاسوب من السنة التي قبلها.
3000 – 2700 = 300 ريال.
c. سعر الحاسوب في عام 1430 هو 900 ريال كما هو واضح
في الشكل في فقرة a.
حدد ما إذا كان AB, CD متوازيين أو متعامدين أو غير ذلك في كل مما
يأتي، ومثل كل مستقيم بيانيا لتتحقق من إجابتك.
22)
A(1,5),B(4,4),C(9,-10),D(-6.-5)
الحل:
23)
A(-6,-9),B(8,19),C(0,-4),D(2,0)
الحل:
24)
A(4.2),B(-3.1),C(6,0),D(-10,8)
الحل:
25)
A(8,-2),B(4,-1),C(3,11),D(-2,-9)
الحل:
26)
A(8,4),B(4,3),C(4,-9),D(2,-1)
الحل:
27) A(4,-2),B(-2,-8),C(4,6),D(8,5)
الحل:
مثل بيانيا المستقيم الذي يحقق الشروط في كل مما يأتي:
28)
يمر بالنقطة A(2,-5)، ويوازي BC، حيث B(1,3), C(4,5).
الحل:
29)
ميله يساوي -2، ويمر بالنقطة H(-2,-4).
الحل:
30)
يمر بالنقطة X(1,-4) ويوازي YZ، حيث Y(5,2),Z(-3,-5).
الحل:
31)
يمر بالنقطة X(1,-4) ويوازي YZ، حيث Y(5,2),Z(-3,-5).
الحل:
32)
سكان: في عام 1412 هـ كان عدد سكان مدينة الطائف 416121 نسمة، وفي عام
1424 هـ بلغ عدد سكانها 521273 نسمة.
a) ما المعدل التقريبي لتغير عدد سكان
مدينة الطائف من عام 1412 هـ إلى 1424 هـ ؟
b) إذا استمر ازدياد عدد السكان بالمعدل
نفسه، فكم نسمة تتوقع أن يبلغ عدد سكان مدينة الطائف عام 1432 هـ ؟
الحل:
a. المعدل
التقريبي لتغير عدد سكان مدينة الطائف من عام 1412 هـ
إلى 1424
هـ يساوي:
b. عدد سكان مدينة الطائف عام 1432 هـ يساوي
(عدد السنوات من عام 1424 إلى عام 1432 X معدل
تغير عدد السكان) + عدد السكان في عام 1424
= (8 سنوات X
8763
)+ 521273
= 70104 + 521273
= 591377 نسمة.
حدد أي المستقيمين في السؤالين الآتيين له أكبر ميل:
33)
المستقيم 1: (0,5) و (6,1).
المستقيم 2: (4,10) و(-8,-5).
الحل:
لإيجاد المستقيم ذو الميل الأكبر يجب علينا حساب الميل لكل مستقيم
منهما
ميل المستقيم 1:
صيغة الميل:
بالتعويض في القانون السابق:
ميل المستقيم 2:
صيغة الميل:
بالتعويض في القانون السابق:
إذا فالمستقيم 2 هو الأكبر.
34)
المستقيم 1: (0,-4) و (2,2)
المستقيم 2: (0,-4) و (4,5).
الحل:
لإيجاد المستقيم ذو الميل الأكبر يجب علينا حساب الميل لكل مستقيم
منهما
ميل المستقيم 1:
صيغة الميل:
بالتعويض في القانون السابق:
ميل المستقيم 2:
صيغة الميل:
بالتعويض في القانون السابق:
إذا فالمستقيم 1 هو الأكبر.
35)
محمية طبيعية: تؤوي محمية طبيعية حيوانا مهددا بالانقراض هو: المها
العربي. ويوضح الشكل المجاور عدد المها العربي في المحمية عامي 1412 هـ و 1415 هـ
.
a) أوجد معدل التغير لعدد حيوانات المها
العربي في المحمية.
b) مثل بيانيا المستقيم الذي يمثل الزيادة
في العدد.
c) إذا استمر النمو وفق هذا المعدل، فكم
يكون عدد حيوانات المها العربي عام 4214 هـ ؟
الحل:
a) معدل
التغير لعدد حيوانات المها العربي في المحمية =
b)
c) عدد حيوانات المها العربي في عام 4214
هـ يساوي
(عدد السنوات من بين عام 1415 وعام 4214
X
معدل التغير في عدد حيوانات المها العربي في المحمية) + عدد حيوانات المها في عام
1415
أوجد قيمة x أو y اعتمادا على المعطيات في كل مما يأتي، ثم
مثل المستقيم بيانيا:
36)
مستقيم يمر بالنقطتين (x,-6) ، (4,-1) ، وميله يساوي -5/2 .
الحل:
37)
مستقيم يمر بالنقطتين (4,3) ، (-4,9) ، ويوازي المستقيم الذي يمر بالنقطتين (-8,1), (4,y).
الحل:
لإيجاد y يجب
إيجاد الميل للمستقيم المار بالنقطتين (4,3) ، (-4,9).
قيمة Y
تساوي:
38)
مستقيم يمر بالنقطتين (1,-3),(3,y) ، و يوازي المستقيم الذي يمر
بالنقطتين (5, -6),(9, y).
الحل:
صيغة ميل المستقيم الأول:
صيغة ميل المستقيم الثاني:
بما أن المستقيم الأول يوازي
المستقيم الثاني فإن ميليهما متساويان (أي لهما نفس الميل)
39)
مدارس: في عام 1421 كان عدد طلاب مدرسة الفتح 1125 طالبا. وفي عام 1427
هـ ازداد عدد الطلاب حتى بلغ 1425 طالبا. وعندما أنشئت مدرسة الأندلس عام 1422 هـ
كان عدد طلابها 1275 طالبا. إذا ازداد عدد طلاب مدرسة الأندلس بنفس معدل زيادة عدد
طلاب مدرسة الفتح، فكم يصبح عدد طلاب مدرسة الأندلس عام 1427 هـ؟
الحل:
معدل زيادة عدد طلاب مدرسة الفتح سنويا:
عدد طلاب مدرسة الأندلس = (عدد
السنوات بين عام 1422 وعام 1427 X معدل زيادة عدد طلاب مدرسة
الفتح) + عدد الطلاب عام 1422
= ) 5 x 50 (+
1275
= 1525
مسائل مهارات التفكير العليا
40)
اكتشف الخطأ: حسب كل من خالد وطارق ميل المستقيم الذي يمر بالنقطتين Q(3,5), R(-2,2)
هل إجابة أي منهما صحيحة؟ وضح تبريرك.
الحل:
إجابة طارق صحيحة. فقد طرح خالد
إحداثيات x
بالترتيب الخاطئ.
41)
تبرير: في المربع ABCD إذا كان A(2,-4), C(10,4).
a) أوجد الرأسين الآخرين B, D للمربع.
b) أثبت أن AB||DC
، AD||BC.
c) أثبت أن قياس كل زاوية من زوايا المربع
يساوي 90.
الحل:
a) B(2,4), D(10, -4).
b) كل من ميلي AB و CD غير
معرف، لذا فهما متوازيان. وميل كل من AD و BC يساوي صفرا، لذا فهما متوازيان.
c) بما أن ميل AB غير
معرف، وميل BC
يساوي صفرا، فإن القطعتين متعامدتان وتشكلان زاوية قياسها 90، وهكذا لبقية
الزوايا.
42)
اكتب: يميل برج بيزا في إيطاليا عن الخط الرأسي بزاوية 3.97. صف ميل كل من برج المملكة و برج بيزا.
الحل:
بما أن برج المملكة رأسي فإن ميله غير معرف، أما ميل برج بيزا فميله
إما أن يكون سالبا أو موجبا بحسب موقع النظر إليه.
43)
تحد: تعلمت في هذا الدرس أن m= y2-y1 / x2-x1.
اكتب برهانا جبريا لتبين أنه يمكن أيضا حساب الميل باستعمال المعادلة m= y1-y2 / x1-x2.
الحل:
تدريب على اختبار
44)
أي المعادلات الآتية تمثل مستقيما يعامد المستقيم الذي معادته y=3/4 x +8؟
a) Y=-4/3 x-6
b) Y= 4/3 x+5
c) Y=3/4 x +1/4
d) Y=-3/4 x-5
الحل:
A
45)
أي القيم الآتية تمثل ميل المستقيم المار بالنقطتين (0,-2)، (2,4) ؟
a) -1/3
b) -3
c) 1/3
d) 3
الحل:
إذا الاختيار الصحيح هوD.
مراجعة تراكمية
في الشكل المجاور: c||d ، a||b، و m<4=57. أوجد قياس كل من الزوايا الآتية:
46)
<5.
الحل:
<5
= 180 – 57 = 123 ، زاويتان متجاورتان ومتكاملتان.
47)
<1.
الحل:
123. 5< = <3
بالتقابل بالرأس، <3 =1> بالتناظر لذا 1> = 123.
48)
<8.
8> = 180 – 123 = 57 ، زاويتان متجاورتان ومتكاملتان.
49)
<10.
الحل:
10> = 8> = 57 بالتبادل داخليا.
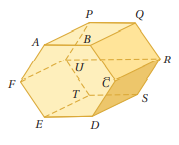
حدد كلا مما يأتي مستعملا الشكل المجاور.
50)
جميع القطع المستقيمة التي توازي TU.
الحل:
BC,EF,QR.
51)
جميع المستويات التي تتقاطع مع المستوى BCR.
الحل:
ABC,ABQ,PQR,CDS.
52)
جميع القطع المستقيمة التي تخالف DE.
الحل:
BQ,CR,FU,PU,QR,RS,TU.
معتمدا على المعطيات، حدد ما إذا كانت النتيجة صحيحة أم لا في كل مما يأتي. فسر تبريرك.
53)
المعطيات: <B,<C متقابلتان بالرأس.
النتيجة: <B=<C
الحل:
صحيحة.
54)
المعطيات: <W=<Y
النتيجة: <W,<Y
زاويتان متقابلتان بالرأس.
الحل:
غير صحيحة، ليس بالضرورة أن تكون الزاويتان المتطابقتان متقابلتين
بالرأس.
استعد للدرس اللاحق:
حل كل معادلة مما يأتي بالنسبة لـ y:
55)
3x+y=5
الحل:
Y=-3x+5
56)
4x+2y = 6
الحل:
2x+y=3
Y=-2x+3
57)
4y -3x=5
الحل:
Y=3/4 x +5/4








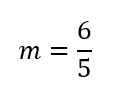















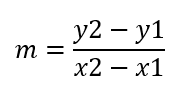







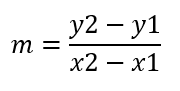



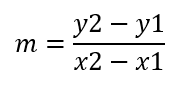




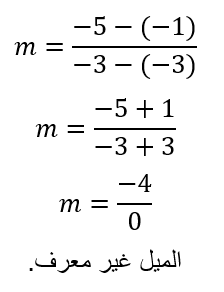




















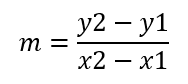


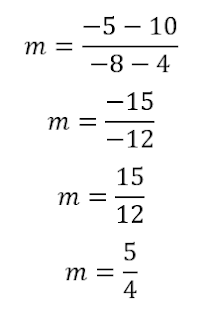


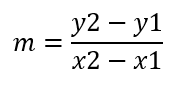
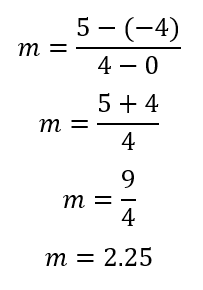









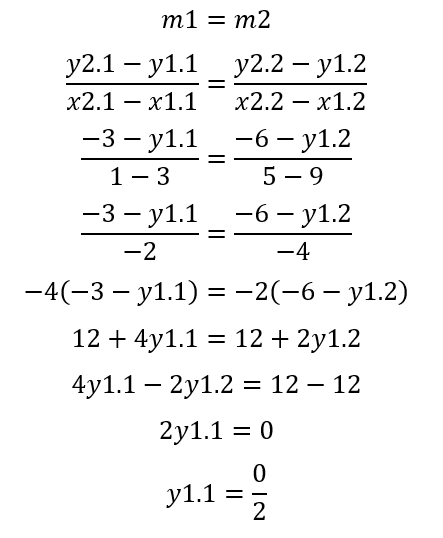

















ليست هناك تعليقات:
إرسال تعليق