إثبات توازي مستقيمين - التوازي والتعامد
· توازي
المستقيمات:
-
مسلمة 1: إذا
قطع قاطع مستقيمين في مستوى وكانت الزوايا المتناظرة متطابقة فإن المستقيمين
متوازيين.
-
مسلمة 2: إذا
علم مستقيم ونقطة لا تقع عليه فإنه يوجد مستقيم واحد فقط يمر بتلك النقطة ويوازي
المستقيم المعلوم.
· خطوات رسم مستقيم مواز لمستقيم معلوم ويمر بنقطة لا تقع عليه:
-
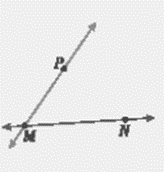
الخطوة 1: أرسم MN
بالمسطرة ثم عين نقطة P لا تقع عليه وارسم PM.
الخطوة 2: ننقل
المثلث PMN
بحيث تكون النقطة P
رأس الزاوية الجديدة ثن نسمي نقطتي التقاطع Q وR.
الخطوة 3: ارسم PQ، بما أن <RPQ=<PMN وهما متناظرتان فإن PQ||MN.
· نظريات إثبات توازي مستقيمان:
-
إذا
قطع قاطع مستقيمان في مستوى، وكانت الزاويتان المتبادلتان خارجيا الناتجتان عن
التقاطع متطابقتين فإن المستقيمين متوازيان.
-
إذا
قطع قاطع مستقيم في مستوى، وكانت الزاويتان المتحالفتان الناتجتان عن التقاطع
متكاملتين فإن المستقيمين متوازيان.
-
إذا
قطع قاطع مستقيمين في مستوى، وكانت الزاويتان المتبادلتان داخليا الناتجتان عن
التقاطع متطابقتين فإن المستقيمين متوازيان.
-
إذا
قطع قاطع مستقيمين في مستوى، وكان عموديا على كل منهما فإن المستقيمين متوازيان.











ليست هناك تعليقات:
إرسال تعليق